trójkąt matix: Oblicz pole trójkąta ABC w którym BC=6 o kątach BCA=120 stopni i ABC=45 stopni

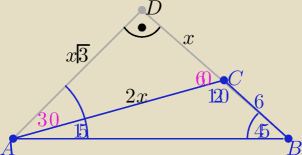
a@b: x√3=x+6 ⇒ x=3(√3+1)

	1
P(ABC)=		*2x*6*sin120o
	2

P(ABC)= 3x√3= ............. i po ptokach

6latek:

	1−cos30o
sin15o= √
	2

Licze sobie na boku

	√3		2−√3		1		2−√3		1−cos300
1−		=		*		=		=
	2		2		2		4		2

	2−√3		√2−√3		√6−√2
√		=		}=		= sin15o
	4		2		4

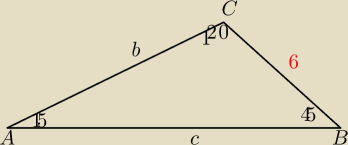
6		b
	=
sin15o		sin45o

	6*sin45o		3√2
b=		=		(tak to zapisze bo zle sie tutaj takie wyrazenia
	sin15o		sin15o

pisze

	12√2		12√2		12
b=		=		=
	√6−√2		√2(√3−1)		√3−1

	12		72		√3
P= 6*		*sin120o=		*		dokoncz
	√3−1		√3−1		2

a@b:

	√2		√3		√2		1		√6−√2
sin15o= sin(45o−30o)=		*		−		*		=
	2		2		2		2		2

6latek: No tak. Masz racje . Nie pomyslalem o tym . Dziękuje.

a@b:

√6−√2
4

chichi:

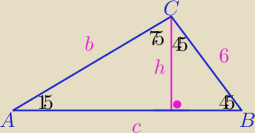
	1		1		√6
(1)		*b*6*sin(120°)=		*c*6*sin(45°) ⇒ b=		c
	2		2		3

(2) c²=b²+6²−2*b*6*cos(120°) ⇒ c²=b²+6b+36

	√6
c2=b2+6b+36 ∧ b=		c
	3

c²−6√6c−108=0, c>0 c=3√6+9√2 (3) h√2=6 ⇒ h=3√2

	1
(4) PΔABC=		*(3√6+9√2)*3√2=27+9√3
	2

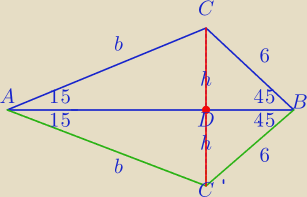Mila: 1) C' − punkt symetryczny do C względem Prostej AB

	62
PΔBCC' =		=18
	2

|CC'|=6√2 2) Z tw. cosinusów w ΔACC': (6√2)²=b²+b²−2b²cos 30^o 72=2b²−b²√3 72=b²*(2−√3) /*(2+√3) 72(2+√3)=b² b²=36*(4+2√3)⇔b=6*√(1+√3)² b=6(√3+1) 3)

	1		1		√3
PΔABC=		b*a sin120o=		*6(√3+1)*6*
	2		2		2

P_ΔABC=9(3+√3) ================

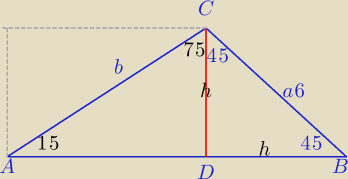Mila: Trochę inaczej niż 6−latek, ale z trygonometrią. 1) ΔCDB− Δprostokątny równoramienny h²+h²=6² h²=18, h=3√2

	√6−√2
2) sin15o=sin(45o−30o)=		Eta zapisała z pomyłką w mianowniku.
	4

W ΔADC:

	h
sin15o=
	b

√6−√2		3√2
	=		⇔ b*(√6−√2=12 √2 /*(√6+√2)
4		b

b*(6−2)=12√2*(√6+√2) b=6(√3+1) 3)

	1		1		√3
PΔABC=		b*a sin120o=		*6(√3+1)*6*
	2		2		2

P_ΔABC=9(3+√3) ================

6latek: Dobry wieczor Milu

Mila: Witam Cię. Jak zdrówko?

a@b: I który sposób najkrótszy ?

6latek: Milu Na razie jestem zdrowy .Nie mam tego wirusa . Milu dbaj o siebie . Chociaz wiem ze to robisz . a@b skoro go uzywasz . Twoj sposob najkrotszy

chichi: @ a@b Oczywiście, że twój, ale przeciętny uczeń na niego nie wpadnie. Ja jeszcze wrzuciłem to jeszcze w układ kartezjański i potraktowałem analitycznie, ale za dużo przepisywania. Zostawię dla siebie, aczkolwiek sposoby @Mila również fajne

kerajs: ''I który sposób najkrótszy ?'' Na razie pierwszy. Dorzucę kolejny sposobik:

	62
P=		=....
	2(ctg 45*+ctg 120*)

kerajs: albo tak:

	62sin 45*sin 120*
P=
	2 sin 15*