geometria Kuba152: W czworościanie o podstawie ABC i wierzchołku D poprowadzono płaszczyznę przechodzącą przez środki krawędzi AB,BD i CD. Płaszczyzna ta dzieli czworościan ABCD na dwie bryły. Jaki jest stosunek ich objętości?

chichi: Próbowałeś coś zrobić sam? Zadanie jest banalne

Mila: Poproś Ite o ilustrację w geogebrze

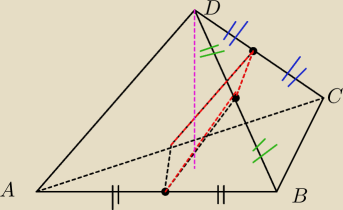
Kuba152: Wiem jak wygląda tylko nie wiem co mam zrobić z krawędzią AC bo nie wiem gdzie przetnie ją płaszczyzna

Kuba152: czy te trójkąty figury są podobne? (tzn czy trójkąt ABD jest podobny do tego ¹₂AB,¹₂BD,B)

Kuba152: Nie no, nawet gdy uznaję że tak to nadal nic nie wychodzi, pomoże ktoś?

chichi: A co ty na to, że przekrojem będzie kwadrat ?

Mila: 1) Środek krawędzi AC również należy do przekroju. 2) Poprowadź pomocniczą płaszczyznę przez środki krawędzi AD,BD i CD. ( otrzymasz przekrój A' B',C') 3) Ustal jaką częścią objętości ostr. ABCD jest ostrosłup A'B'C'D" Jeśli będziesz miał kłopoty , to pomogę. Pisz.

Kuba152: @Mila

A'B'C'D		1
	=		?
ABCD		8

Mila: Dobrze Dalej co widzisz?

chichi: @Mila Albo już dziś źle myślę, albo czy aby na pewno twoje rozwiązanie prowadzi do tego o co nas proszą? Czy stosunek, który podajesz w 3 punkcie będzie tym prawidłowym stosunkiem? Sprawdź proszę jeszcze raz swoje rozważania i daj znać czy ja źle myślę czy ty

chichi: 00:01 @Mila cofam moją wypowiedź, bo tak ładnie w podpunktach rozpisałaś jakby to miał być plan na całe zadanie hah, myślałem, że miałaś na myśli, że stosunek z 3) to odpowiedź do zadania, miłej nocy

Mila: A co ty myślisz chichi ? Uzupełniłeś rysunek , jak radziłam? Ja tam widzę z lewej strony graniastosłup pochyły o znanej podstawie i wysokości.

Kuba152:

	5
Coś dalej źle robię bo stosunek mi wychodzi
	8

Mila: JUż rysuję.

chichi: @Mila Myślałem, że twoje 3 podpunkty z 23:48 to koniec zadania dlatego zapytałem Ale po twojej wypowiedzi z 00:01 wywnioskowałem, że to nie koniec, dlatego od razu napisałem komentarz z 00:05

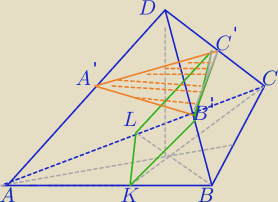
Mila: V− objętość ostrosłupa ABCD 1)

	1
ΔA'B'C'∼ΔABC w skali k=
	2

	1
VA'B'C'D=		V
	8

2) Graniastosłup (pochyły) AKLA'B'C' ΔAKL≡ΔA'B'C' Wysokości A'B'C'D i AKLA'B'C' ⇔

	1
Vgran=3*		V
	8

	1		3		1
3) V−(		V+		V)=		V⇔
	8		8		2

KB'C'L dzieli dany ostrosłup na bryły o jednakowej objętości. ===========================================

Mila: Dobranoc No to, do jutra

Kuba152: @Mila Dziękuję Ci bardzo za takie ładne rozwiązanie! Dobranoc

Mila: No mój rysunek gorszy od Twojego, ale coś tam widać

Kuba152: Wszystko dobrze widać!

	1
Pomyliłem się przy tym graniastosłupie pochyłym i liczyłem 2*		V, zamiast 3
	8

Jeszcze raz dziękuję!

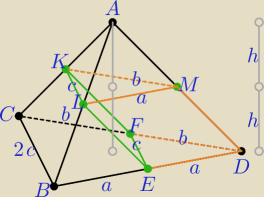
Bogdan: Nic nowego co stwierdziła Mila nie dodam, powtarzam to rozwiązanie w takim ujęciu:

	V
skala podobieństwa trójkątów CBD i KLM: k = 2, stąd		= k3 = 8
	V0

V₀ − objętość ostrosłupa KLMA oraz V = 8V₀ − objętość ostrosłupa CBDA V_G = 3V₀ − objętość pochyłego graniastosłupa FEDKLM

	1
VB = V − VG − V0 = 8V0 − 3V0 − V0 = 4V0 =		V − objętość bryły CBEFKL
	2

Mila: Zawsze to lepiej wygląda bez ułamków i rysunek piękny Pozdrawiam.