Na dowodzenie Alaias: Dany jest czworokąt ABCD . Niech będzie S punktem przecięcia jego przekątnych. Udowodnij, że czworokąt ABCD można wpisać w okrąg wtedy i tylko wtedy, gdy |AS|/|DS|=|BS|/|CS|.

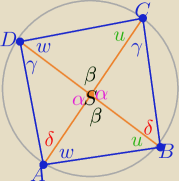
a@b: 1/ trójkąty ASD i BSC są podobne z cechy (kbk) bo mają proporcjonalne boki ( z treści zadania) i kąty między nimi mają równe miary α zatem mają też równe kąty o miarach γ iδ 2/ z treści zadania

AS		BS		AS		DS
	=		⇒		=
DS		CS		BS		CS

zatem podobne są też trójkąty ABS i CDS z cechy (kbk) bo kąty między tymi bokami mają miary równe β zatem kąty w i u w tych trójkątach mają równe miary i mamy tezę : sumy kątów przeciwległych są równe 180^o ( δ+w+u+γ=180^o Na takim czworokącie można opisać okrąg ==================================

a@b: Poprawiam zapis: oczywiście z cechy (bkb)