Nierówność, wartości bezwzględne Szkolniak:

	|x|		|x−2|		|x−1|
Rozwiąż nierówność:		+		<1+
	x		x−2		x−1

Określamy dziedzinę nierówności: x∊D=ℛ\{0,1,2} Można to rozwiązać rozpatrując 8 przypadków, ale zdecydowałem że to za dużo i w sumie poszedłem w inną stronę. Rozwiązałem to tak: Lewa strona nierówności może przyjmować trzy wartości: −2, 0, 2 Natomiast prawa może przyjmować dwie wartości: 0, 2 Aby nierówność była spełniona, L<P, a to zachodzi wtedy, gdy: 1) L=−2 ∧ P∊{0,2} 2) L=0 ∧ P=2 1.1) L=−2 ⇔ x<0 i x<2 ⇔ x<0 P=0 ⇔ x<1 zatem: x<0 1.2) L=−2 ⇔ x<0 P=2 ⇔x>1 zatem: x∊∅ 2) L=0 ⇔ (x<0 i x>2) lub (x>0 i x<2) ⇔ x∊(0;2) P=2 ⇔ x>1 zatem: x∊(1;2) Biorąc sumę wszystkich przypadków: x∊[(−inf;0)∪(1;2)]⊂D Jest okej? I czy jest może jakiś sprytniejszy sposób na rozwiązanie tego?

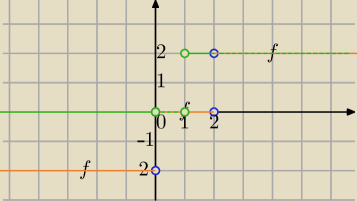
Mila: D=R\{0,1,2} Graficznie :

	|x|		|x−2|
f(x)=		+
	x		x−2

1) f(x)=−1+(−1)=−2 dla x<0 lub f(x)=1+(−1) = 0 dla x∊(0,2) lub f(x)=1+1 =2 dla x∊ (2,∞)

	|x−1|
2) g(x)=1+
	x−1

g(x)=1+(−1) =0 dla x<1 g(x)=1+1=2 dla x>1 f(x)<g(x) dla x∊(−∞,0)∪(1,2) Przerywaną zieloną linią zaznaczono tam, gdzie wykresy pokrywają się.

Szkolniak: Rzeczywiście, coś mi często umykają te sposoby graficzne i zapominam o tym.. Dziękuję Mila!

a@b: W czym trudność z przedziałami ? D=R\{0,1,2} x∊(−∞,0) −1−1<1−1 ⇒ −2<0 odp: x∊(−∞,0) x∊(0,1) 1−1<1−1 sprzeczność x∊(1,2) 1−1<1+1 ⇒ 0<2 odp: x∊(1,2) x∊(2,∞) 1+1<1+1 sprzeczność Odp: x∊(−∞,0) U (1,2)