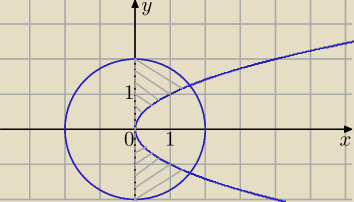
Nierówności Szkolniak: Zaznacz w układzie współrzędnych zbiór wszystkich par (x,y) liczb rzeczywistych, dla których wyrażenie:

	1
4√4−x2−y2−		ma wartości rzeczywiste.
	√y−log2(x)

Określamy dziedzinę: 4−x²−y²≥0 ∧ y−log₂(x)>0 ∧ x>0 x²+y²≤4 ∧ y²>x ∧ x>0 Okrąg rysowany linią ciągłą, funkcja x=y² rysowana linią przerywaną, a jeśli chodzi o ten warunek x>0? Czy mogę to zrobić w ten sposób jak na rysunku? Czyli rysujemy obie osie i tam na odcinku od y=−2 do y=2 linia przerywana? Czy jak to inaczej rozwiązać?

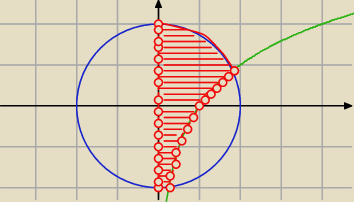a@b: x²+y²≤4 ∧ y>log₂x ∧ x>0

Szkolniak: Rzeczywiście, coś namieszałem, nie wiem skąd ja to wziąłem.. Dzięki piękne.