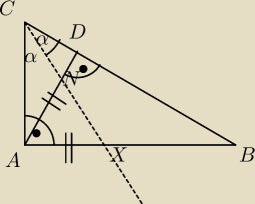
 Niech ABC będzie trójkątem prostokątnym z kątem prostym przy wierzchołku A i niech AD będzie
wysokością opuszczoną na przeciwprostokątną. Punkt N jest punktem przecięcia AD oraz
dwusiecznej
kąta przy wierzchołku C. Udowodnić, że długości odcinków spełniają równość:
|AD| · |BC| = |AB| · |DC| + |BD| · |AN|.
Rysunek załączam powyżej. Próbowałem z podobieństwa trójkątów AXN∼CND albo ABC∼ADC ale nic
mi nie wychodzi
Mógłby ktoś udzielić mi jakiś wskazówek jak mam to zrobić?
Niech ABC będzie trójkątem prostokątnym z kątem prostym przy wierzchołku A i niech AD będzie
wysokością opuszczoną na przeciwprostokątną. Punkt N jest punktem przecięcia AD oraz
dwusiecznej
kąta przy wierzchołku C. Udowodnić, że długości odcinków spełniają równość:
|AD| · |BC| = |AB| · |DC| + |BD| · |AN|.
Rysunek załączam powyżej. Próbowałem z podobieństwa trójkątów AXN∼CND albo ABC∼ADC ale nic
mi nie wychodzi
Mógłby ktoś udzielić mi jakiś wskazówek jak mam to zrobić?
| |AD| · |BC| | |AB| · |DC| | |BD| · |AN| | |||
= | + | ||||
| 2 | 2 | 2 |
| sin α | ||
|AN|=|AC| | ||
| sin (90+α) |
