trojkat rownoboczny Struś pędziwiatr: Mamy dane dwa wierzcholki z₁ i z₂ trojkata rownobocznego Znalezc trzeci wierzcholek Czy jest inny sposob oprocz wyznaczenia symetralnej i policzenia punktow przeciecia okregu z symetralna ? dziekuje .

ICSP: ustaw swój odcinek tak aby zaczynał się w pkt (0,0) Następnie dokonaj obrotu o 60^o w obie strony. Na koniec dokonaj odpowiedniej translacji aby z (0,0) wrócić na z₁.

Struś pędziwiatr: Sprobuje tak zrobic

Struś pędziwiatr: Zadanie bylo z paragrafu Postac trygonometryczna liczby zespolonej Znalazlem odpowiedz

	1		√3
z3= z1+(z2−z1)(		±i		)
	2		2

Moze ktos wytlumaczyc bo nie rozumiem tego

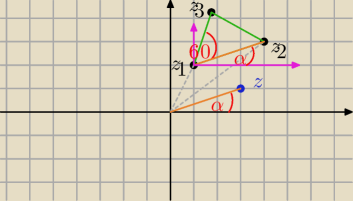
luui: z₂ − z₁ // (niebieskie z) jest to bok trójkąta między z₁ a z₂, tylko odłożony względem początku układu współrzędnych.

1		√3
	± i		= 1*(cos(60o) ± isin(60o)) // moduł wynosi 1, więc w wyniku iloczynu
2		2

zmieni się tylko argument niebieskiego punktu: α ± 60^o = arg(z₃) // kąt nachylenia z₃ do osi OX' (nowej osi, której początek układu współrzędnych znajduje się w miejscu z₁). W związku z czym:

	1		√3
(z2 − z1)(		± i		) // jest punktem z3,
	2		2

ale w nowym układzie współrzędnych.

	1		√3
Dlatego do (z2 − z1)(		± i		) dodaje się z1, aby nasze z3 było określone w
	2		2

tym czarnym układzie współrzędnych.

Struś pędziwiatr: Bardzo Ci dziekuje