Który z trapezów równoramiennych opisanych na okręgu o promieniu długości r ma n mjm: Który z trapezów równoramiennych opisanych na okręgu o promieniu długości r ma najmniej− sze pole? Wyznacz to pole. Witam, kompletnie nie wiem jak zabrać się za to zadanie, za pomoc z góry dziękuję

Filip: To bedzie kwadrat

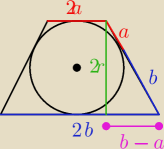
Saizou : Z tw. Pitagorasa 4r² + (b−a)² = (b+a)² 4r² = 4ab r² = ab Dalej kombinuj

mjm: okej ale dlaczego tak będzie ?

Saizou : Którego momentu nie rozumiesz? Wiesz skąd bierze się różowy odcinek o długości b−a? Wiesz skąd bierze się ramie o długości a+b? (tw. o dwóch stycznych do okręgu)

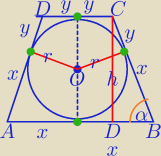
Mila: h=2r p=2x+2y P_ABCD=p*r=(2x+2y)*r P_ABCD=2r*(x+y) W ΔCDB: |DB|=x−y

	2r
sinα=
	x+y

	2r
x+y=
	sinα

	2r		4r2
P(α)=2r*		=
	sinα		sinα

	π
największa wartość sinα dla α=		wtedy x+y=2r
	2

	π		x−y
cos		=0=
	2		x+y

x−y
	=0⇔x−y=0⇔x=y
2r

P=4r²− najmniejsze pole ABCD, gdy jest kwadratem o boku 2r.

Saizou :

	1
P(a,b,r) =		(2a+2b)r = 2ar + 2br
	2

Am ≥ Gm

2ar+2br
	≥ √4abr2 = √4r4 = 2r2
2

2ar+br ≥ 4r² P ≥ 4r² Równość zachodzi dla a =b

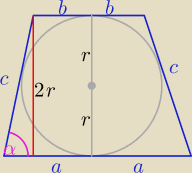
Eta: Z warunku wpisania okręgu w trapez

	2r		2r
c=a+b sinα=		⇒ a+b=
	c		c

	4r2
P(α)=		dla sinα=1 czyli α=90o
	sinα

pole jest najmniejsze i P=4r² czyli taki trapez jest kwadratem o boku 2r

Eta:

	2r
Poprawiam zapis a+b=
	sinα