Wyznaczyć punkty A i B wiedząc, że ... etna:

	3
Wyznaczyć punkty A i B wiedząc, że punkt C(−5,4) dzieli odcinek AB w stosunku		, a punkt
	4

	2
D(6,−5) w stosunku		.
	3

Qulka: A(94;−77) B(−38;31)

Eta: A ja mam: A(160, −131) B(−225,184)

Qulka: a mi teraz wyszło odwrotnie A(−38;31) B(94;−77)

Qulka: znalazłam błąd jednak jak na początku

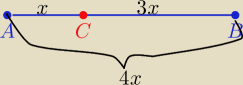
Eta: Quleczko rys. w/g Twoich obliczeń

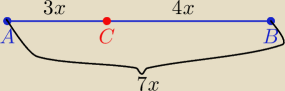
Eta: Rys. w/g moich obliczeń

Qulka: tych na początku? ? bo tamte są dobrze czyli A jest dalej niż C

Qulka: bo ja widziałam tam ułamek czyli 3/4 nie wpadłam na to że to 3:4 ... ech ta precyzja zapisu przez pytających

Eta: Sprawdzamy: Prosta AB=prosta CD : 9x+11y+1=0 A(160,−131) ∊ CD bo 1440−1441+1=0 B(−225,184) ∊ CD bo −2025+2024+1=0

Eta: No to teraz i ja też już nie wiem? jaki jest ten stosunek ?

ABC: nie ważne jaki stosunek ważne żeby dzieci zdrowe się urodziły

Eta:

Filip:

KLZ: Mam napisane w ksiazce tak

	1
1:4=
	4

Moge poprosic o obliczenia lub przynajmniej wzory do obliczenia ? Dziękuje .

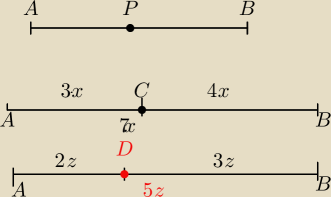
KLZ: Jesli k to stosunek podzialu odcinka to

	xA+k*xB
xP=
	1+k

	yA+k*yB
yP=
	1+k

Tu jest odcinek AB . Musi byc 7x=5z Chcac skorzystac z tych wzorow mam dwie niewiadome i sie odrobine komplikuje .

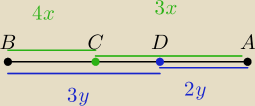
Qulka: wspólny mianownik 3 i 7 to 35 więc x=5 y=7 BC=20/35 AB BD=21/35 AB toteż CD=1/35 AB = [11;−9] zatem AB=[375;−99] DA= 14/35 AB = 14CD = [154;−126] A=(6+154;−5−126) = (160;−131) BD=21CD=[231;−189] B=(6−231;−51(−189))=(−225;184)

Qulka: nie komplikuj ... u Ciebie x=5 z=7

KLZ: Dziękuje i dobrej nocy .

Mila: 1) A=(a₁,a₂), B=(b₁,b₂), C=(c₁,c₂)=(−5,4), D=(d₁,d₂)=(6,−5) − punkty podziału

	3		2
AC→=		CB→ i AD→=		DB→
	4		3

2) Współrzędne punktów podziału: C:

	3
[c1−a1,c2−a2]=		[b1−c1, b2−c2] ⇔
	4

	3		3
c1−a1=		b1−		c1
	4		4

	3		3
c2−a2=		b2−		c2
	4		4

===================⇔

	3		4
c1=		b1+		a1
	7		7

	3		4
c2=		b2+		a2
	7		7

===================== D:

	2		2
AD→=		DB→⇔[d1−a1,d2−a2]=		[b1−d1,b2−d2]
	3		3

wyznaczamy wsp. D w podobny sposób jw. mamy:

	2		3
d1=		b1+		a1
	5		5

	2		3
d2=		b2+		a2
	5		5

==================== 3) Mamy układy równań: (1)

	3		4
−5=		b1+		a1
	7		7

	2		3
6=		b1+		a1 stąd: a1=160 i b1=−225
	5		5

(2)

	3		4
4=		b2+		a2
	7		7

	2		3
−5=		b2+		a2 stąd: a2=−131, b2=184
	5		5

4) A=(160,−131), B=(−225,184) ==========================

KLZ: Dziękuje i miłego wieczoru życzę

Mila:

Eta: Ja liczyłam tak: C −− punkt podziału odcinka AB w stosunku k>0

	xA+k*xB		yA+k*yB
xC=		i yC=
	k+1		k+1

=========================

	3		2
dla k=		i C(−5,4) i dla k=		i D(6,−5) mamy:
	4		3

7*(−5)=4x_A+3x_B /*(−2) i 7*4=4y_A+3y_B /*2 5*6=3x_A+2x_B /*3 i 5*(−5)=3y_A+2y_B /*(−3) 70=−8x_A−6x_B i 56= 8y_A+6y_B 90= 9x_A+6x_B i 75=−9y_A−6y_B −−−−−−−−−−−−− i −−−−−−−−−− x_A=160 i y_A= −131 to x_B=−225 to y_B= 184 A( 160,−131) , B( −225,184) =================================

KLZ: Dziękuje.