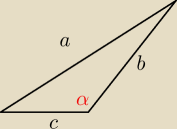
wykaż Kuba152: Wykaż, że jeśli w trójkącie o bokach a, b, c i polu 1 zachodzi a ≥ b ≥ c to b ≥ √2. Nie wiem czy źle robię czy jest błąd w zadaniu:

	1
P=		bc sin α = 1
	2

bc sin α = 2 sin α ≤ 1 bc ≤ 2 c≤b b² ≤ 2 b ≤ √2

Jerzy:

	1
Dla tego trójkąta P =		c*b*sin(90 − α)
	2

Kuba152: coś mi nie wychodzi, Mógłbyś rozpisać jak dalej?

Jerzy:

	1
Pomyłka , P =		c*b*sin(180 − α)
	2

ICSP: z tego, że bc ≤ 2 ∧ c ≤ b nie wynika, że b² ≤ 2 prosty przykład: c = 1 , b = 2 wtedy bc = 2 ≤ 2 ∧ 1 ≤ 2 ale już b² = 4 ≥ 2

ICSP: kolejny błąd: bcsinα = 2 i sinα ≤ 1 więc skoro sinα jest mniejszy od jeden to aby cały iloczyn dał 2 to bc musi być większe od 2: bc ≥ 2

ICSP: Jednak sam pomysł na rozwiązanie jest jak najbardziej poprawny. Błędy są czysto logiczne/rachunkowe.

Kuba152: aaa, rozumiem Dziękuję Ci bardzo!