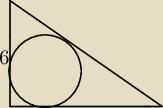
okrąg wpisany w trójkąt niekumaty: Witajcie matematyczni geniusze Mam takie zadanie: W trójkącie prostokątnym krótsza przyprostokątna ma długość 6, a jeden z kątów ma miarę 60 stopni. Oblicz długość okręgu wpisanego w ten trójkąt.

edi:

	P
promień okręgu wpisanego w trójkąt wynosi
	p

Gdzie P to pole trójkąta, a p to połowa obwodu Za pomocą funkcji trygonometrycznych liczymy miary pozostałych boków: dłuższa przyprostokątna: 6√3 przeciwprostokątna: 12 P=18√3 p=3(3+√3)

P		18√3
	=		= 3(√3 − 1)
p		3(3+√3)

niekumaty: nie mam pojęcia, skąd wziąłeś połowę obwodu ale dziękuję bardzo za obliczenia

niekumaty: ktoś wie jak dojść do takich obliczeń?

edi: http://pl.wikipedia.org/wiki/Tr%C3%B3jk%C4%85t#Pole_powierzchni