prawdopodobienstwo kasia0948: W pudełku znajduje się 30 piłeczek ponumerowanych 1,2,3,...,30. Losujemy kolejno dwie piłeczki bez zwracania. Oblicz prawdopodobieństwo zdarzenia, że druga wylosowana piłeczka jest liczbą pierwszą, jeżeli wiadomo, że pierwsza piłeczka była oznaczona nieparzystą liczbą. Wypisałam sobie te liczby, ale nie wiem jak dalej, nie miałam jeszcze rachunku prawdopodobieństwa na lekcjach Liczby nieparzyste: 1,3,5,7,9,11,13,15,17,19,21,23,25,27,29 Liczby pierwsze: 2,3,5,7,11,13,17,19,23,29 Jak obliczyć tutaj omegę i zdarzenie A ?

Jerzy: To skąd wiesz,że trzeba obliczyć moc Ω i moc A ?

kasia0948: Robiłam prostsze zadania na rzut kostką i rzut monetą

kerajs: To prawdopodobieństwo warunkowe.

	9*9+6*1030*29
P(A|B)=P(A∩B)P(B)=
	1530

kasia0948: Dziękuję kerajs, poczytam o prawdopodobieństwie warunkowym

BoosterXS: Jak powstał licznik tego ułamka? P(A∩B) = P(A) + P(B) − P(A∪B)

	10		1
P(A) =		=
	30		3

	15		1
P(B) =		=
	30		2

	|A∪B|		9
P(A∪B) =		=
	|Ω|		30

Nie zgadza się to z liczbami podanymi wyżej, ale wiem, że gdzieś mam błąd, bo finalne prawdopodobieństwo wychodzi >1

Mila: A− Druga wylosowana piłeczka jest liczbą pierwszą, jeżeli wiadomo, że pierwsza piłeczka była oznaczona nieparzystą liczbą. B− pierwsza piłeczka była oznaczona nieparzystą liczbą (druga dowolna ) |B|=15*29 A∩B−pierwsza wylosowana nieparzysta ale nie pierwsza i druga jest liczbą pierwszą lub pierwsza wylosowana nieparzysta i pierwsza i druga wylosowana jest liczba pierwszą Liczby nieparzyste: 1,3,5,7,9,11,13,15,17,19,21,23,25,27,29 Liczby pierwsze: 2,3,5,7,11,13,17,19,23,29 Liczby nieparzyste ale nie pierwsze 1,9,15,21,25,27 |A∩B|=6*10+9*9=60+81=141

	|A∩B|		141		47
P(A/B)=		=		=
	|B|		15*29		5*19

Nie wiem, czy nie pomyliłam się Sprawdzajcie maturzyści.

chichi: @Mila, a studenci też mogą?

141		47
	≠
15*29		5*19

	141		47		47
Raczej powinno być:		=		=
	15*29		5*29		145

Filip: Cześć chichi, jak tam idą zaliczenia przedmiotów na studiach?

Mila: Mogą, mogą. Trzeba uważać na klawisze, "chochliki" się pojawiają.

chichi: Cześć, @Filip, a bardzo dobrze Niektóre 5 z ćwiczeń przepisują mi na ocenę z egzaminu, a z niektórych mimo bardzo dobrej oceny muszę przystąpić do egzaminu czyli z analizy matematycznej i ze wstępu do algebry i teorii liczb A jak u Ciebie? @Mila Aczkolwiek wynik się zgadza, też mi tak wyszło

Filip: Mnie właśnie czeka egzamin z analizy i podstaw informatyki, wszystko jednego dnia Przedmioty jako tako zaliczone − jeszcze nie wszystkie. We środę poprawiam zarządzanie projektami. Właśnie będę robić prezentację + kilkunastu stronnicowy dokumenty Na jaką ocenę to nie wiem, ważne aby przebrnąć przez pierwszy rok, bo jest sporo bezużytecznych przedmiotów

chichi: @Filip trzymam kciuki, na pewno dasz radę

Filip: Ja mam tak pojebane rzeczy teraz na analizie, jakieś szeregi Fouriera

chichi:

winx: to jaki jest wynik w końcu

0scarit0: nie rozumiem jak obliczyliście |A∩B|, czy ktoś może wytłumaczyć?

rambambam: a czy można zrobić to zadanie na drzewku?

winx: @rambambam nie wiem

rambambam: @winx ok

baltiza: nie rozumiem tego zadania w ogóle ! o co w tym chodzi ?

rambambam: @baltiza ja też

baltiza: a dobra, już rozumiem

winx:

rambambam: @baltiza to wytłumacz

winx: ale to jak w końcu?

baltiza: nie umiem tłumaczyć niestety

Mila: A∩B|=6*10+9*9=60+81=141 6*10 − pierwsza liczba ze zbioru: {1,9,15,21,25,27} druga ze zbioru: {2,3,5,7,11,13,17,19,23,29} 9*9− pierwsza wylosowana ze zbioru liczb pierwszych bez 2. druga z pozostałych w zbiorze liczb pierwszych

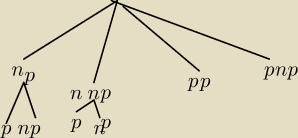
Olga: Proszę o pomoc, próbowałam to zrobić drzewkiem stochastycznym, ale wychodzi mi dwukrotnie za mały wynik. Podzieliłam liczby na nieparzyste pierwsze (np) jest ich 9, nieparzyste nie−pierwsze, jest ich 6 razem z 1. Później z nieparzystych pierwszych losuję jeszcze jedną z 9 pierwszych (dochodzi 2), a z nieparzystych nie−pierwszych jedną z 10 (też z 2). Wychodzi mi wynik 141/870, czyli dokładnie dwa razy mniejszy.

wredulus_pospolitus: Błąd został popełniony już na samym początku −−− w drzewku nie ma 'miejsca' na pp i pnp Zadanie mówi o sytuacji gdy wiemy, że pierwsza kula jest nieparzysta. O co mi chodzi ... zapewne policzyłaś prawdopodobieństwa na gałęzi 'do np' oraz 'do nnp' jako:

	9		6
odpowiednio		oraz		i tu właśnie popełniasz błąd.
	30		30

	9		6
te wartości winny wynosić:		i		ponieważ pierwsze losowanie 'jest
	15		15

tylko z kul nieparzystych' (tak ... w urnie jest 30 kul ... ale WIEMY, że w pierwszym losowaniu wylosowano nieparzystą ... związku z tym 'tak jakby' zapominamy na ten moment o wszystkich parzystych liczbach) To zadanie jest z prawdopodobieństwa warunkowego i może być Ci ciężko to zrozumieć rysując drzewko w taki sposób jak narysowałaś.

Mila: Spróbuję narysować to trochę okaleczone "drzewko", ale później.

Olga: Bardzo dziękuję za wyczerpującą odpowiedź @wredulus−pospolitus

wredulus_pospolitus: Olga ... alternatywnie możemy myśleć w ten sposób: Informacja, że w pierwszym losowaniu wyciągnięto nieparzystą 'zmienia' nam zadanie w: W urnie mamy 15 ponumerowanych kul. Numery to kolejne liczby nieparzyste. Po wyciągnięciu jednej kuli dorzucamy do urny 15 ponumerowanych kul, numery to kolejne liczby parzyste. Następnie losujemy jedną kulę. Oblicz prawdopodobieństwo, że wylosowaliśmy kulę której numer to liczba pierwsza. Przy okazji −−− jeżeli zrozumiesz zasadę, jak 'dodatkowa informacja' (w tym przypadku: "w pierwszym losowaniu wyciągnięto kulę o nieparzystym numerze") zmienia sposób w jaki liczymy prawdopodobieństwo ... wszelkie zadania z prawdopodobieństwa WARUNKOWEGO staną się dla Ciebie bardzo proste.