jakobian salamandra: Wyznacz jakobian funkcji a) f(x,y)=(xsiny, xcosy) Jf(x)−> = | siny x*cos y | | cosy x*siny | b) f(x,y,z)=(xlny, xyz, x^z)

	x
Jf(x)−> = | lny		0 |
	y

| yz xz xy | | x^z−1 0 lnx*x^z | Czy to jest dobrze? Nie wiedziałem jak na forum inaczej oznaczyć tę macierz (to wszystko jest w jednej macierzy)

Saizou : f(x,y) = (xsiny, xcosy) f₁(x,y) = xsiny f₂(x,y) = xcosy Tworzymy macierz Jacobiego (dla funkcji f: R² → R²)

(df1/dx) (df1/dy) (df2/dx) (df2/dy)

Wyznacznik tej macierzy nazywamy jakobianem.

salamandra: Teorie znam, ale nie wiem, czy dobrze to zrobiłem

Saizou :

df1		df1
	= siny		= xcosy
dx		dy

df2		df2
	= cosy		= −xsiny
dx		dy

	siny xcosy cosy −xsiny
det		= −xins2y − xcos2y = −x(sinx2y+cos2y)= −x

salamandra: Tak, o minusie zapomniałem jednym. A już stricte w tej macierzy, jak się z niej "wychodzi"? Tak jak zrobiłeś w ostatniej linijce? Akurat tego nie miałem podane nigdzie

Saizou : Po prostu obliczyłem wyznacznik tej macierzy zobacz na początek, że napisałem że liczę wyznacznik

	.. .. .. ..
det

salamandra: Nie miałem wyznaczania wyznaczników podanych, więc nie wiedziałem, skąd to wziąłeś

Saizou :

	a b c d
det		= ad − cb

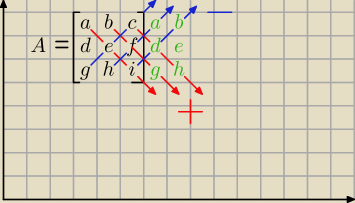
dla macierzy 3x3 zastosuj metodę Sarrusa Dopisuję dwie kolumny z prawej strony (pierwszą i druga), następnie mnożę wzdłuż przekątnych. Czerwone przekątne dodaje, niebieskie odejmuję. det A = aei + bfg + cdh − gec − hfa − idb Wyznacznik oznaczamy jako det A lub |A|

salamandra: dzięki