równanie z pierwiastkiem Ktoś inny: rozwiąż rónanie x²−4x+5=√x−1

Jerzy: Zacznij od ustalenia dziedziny.

Jerzy: Dla nieujemnej lewej strony podnieś obie strony do kwadratu.

ABC: jedź analizą starożytnych a na końcu zobaczysz czy kandydaci na pierwiastki spełniają i siedzą w dziedzinie

Ktoś inny: dziedzinę znam mam posatać x⁴−16x³+96x²−129x+260=0 nie wiem co z tym począć

Ktoś inny: x⁴−16x³+96x²−257x+260

wmboczek: łatwiej będzie znaleźć pierwiastki gdy podstawimy √x−1=t

ABC: to ja proponuję x−2=t , wtedy x²−4x+5=t²+1 , x−1=t+1

Eta: x=2 lub ....

Mariusz: Kilka sposobów na to równanie masz tutaj http://matwbn.icm.edu.pl/ksiazki/mon/mon11/mon1110.pdf To równanie możesz też rozwiązać w ten sposób Wielomian a₄x⁴x+a₃x³+a₂x²+a₁x+a₀

	a3
zapisujesz w postaci sumy potęg dwumianu (x+		)
	4a4

Odpowiednie współczynniki możesz uzyskać stosując kilkukrotnie schemat Hornera Otrzymasz równanie

	a3		a3		a3
(x+		)4+b2(x+		)2+b1(x+		)+b0=0
	4a4		4a4		4a4

	a3
Następnie podstawiasz y=x+
	4a4

Otrzymujesz równanie y⁴+b₂y²+b₁y+b₀=0 Wielomian y⁴+b₂y²+b₁y+b₀ można zapisać jako iloczyn dwóch trójmianów Porównując współczynniki przy wielomianach y⁴+b₂y²+b₁y+b₀ oraz (y²−py+q)(y²+py+r) Otrzymujesz układ równań którego rozwiązanie da ci rozkład na iloczyn dwóch trójmianów kwadratowych A może wystartować jak w metodzie ogólnej ? x⁴−16x³+96x²−257x+260=0 (x−4)⁴=x⁴−16x³+96x²−256x+256=0 (x−4)⁴−(x−4)=x⁴−16x³+96x²−257x+260 (x−4)⁴−(x−4)=0 (x−4)((x−4)³−1)=0 No okazało się że nie musimy dalej stosować metody ogólnej bo udało nam się wyciągnąć wspólny czynnik i dalej już widać wzór skróconego mnożenia (x−4)((x−4)³−1)=0 (x−4)(x−4−1)((x−4)²+(x−4)+1)=0 (x−4)(x−5)(x²−8x+16+x−4+1)=0 (x−4)(x−5)(x²−7x+13)=0 Δ=49−4*1*13=−3<0

Mariusz: Jak teraz to sobie sprawdzałem to o godzinie 10 gru 2020 18:56 chciałeś rozwiązywać inne równanie No Eta jaki będzie ten drugi pierwiastek ?

6latek: Rownanie bedzie wygladalo tak x⁴−8x³+26x²−41x+26=0

jc: x²−4x+5=√x−1 (x−2)²+1 = √(x−2)+1 y=x−1 y²+1=√y+1 y⁴+2y²+1=y+1 0=y⁴+2y²−y=y(y³+2y²−1)=y(y³+y² + y² + y − y −1)=y(y+1)(y²+y−1) y=0, y=−1, ... i sprawdzamy, które liczby faktycznie są rozwiązaniami

jc: Oj, oczywiście y=x−2.

Mariusz: 6latek, tak i gdybyś chciał to rozwiązywać w sposób ogólny to x⁴−8x³+26x²−41x+26=0 (x⁴−8x³)−(−26x²+41x−26)=0 (x⁴−8x³+16x²)−(−10x²+41x−26)=0 (x²−4x)²−(−10x²+41x−26)=0

	y		y2
(x2−4x+		)2−((y−10)x2+(−4y+41)x+		−26)=0
	2		4

Δ=0

	y2
4(		−26)(y−10)−(−4y+41)2=0
	4

(y²−104)(y−10)−(16y²−328y+1681)=0 (y³−10y²−104y+1040)−(16y²−328y+1681)=0 y³−26y²+224y−641=0 No i tutaj rozwiązanie się komplikuje Gdy zastosujemy inny sposób rozwiązania , lubiany przez fanów metody współczynników nieoznaczonych to przypadkowo dostaniemy jedno rozwiązanie x⁴−8x³+26x²−41x+26=0 Przedstawmy wielomian x⁴−8x³+26x²−41x+26 w postaci sumy potęg dwumianu x−2 aby wyrugować wyraz z x³ i uprościć równanie rozwiązujące 1 −8 26 −41 26 2 1 −6 14 −13 0 2 1 −4 6 −1 2 1 −2 2 2 1 0 2 1 x⁴−8x³+26x²−41x+26=(x−2)⁴+2(x−2)²−(y−2) (x−2)⁴+2(x−2)²−(x−2)=0 Jeśli teraz przyjmiemy że y=x−2 to otrzymamy y⁴+2y²−y=0 Widzimy że y=0 jest pierwiastkiem ale zastosujmy dalej metodę ogólną y⁴+2y²−y=(y²+ay+b)(y²+cy+d) y⁴+2y²−y=y⁴+cy³+dy²+ay³+acy²+ady+by²+bcy+bd y⁴+2y²−y=y⁴+(a+c)y³+(b+d+ac)y²+(ad+bc)y+bd a+c=0 b+d+ac=2 ad+bc=−1 bd=0 c=−a b+d=2+a² a(b−d)=1 4bd=0 c=−a b+d=2+a²

	1
b−d=
	a

4bd=0 c=−a

	1
2b=2+a2+
	a

	1
2d=2+a2−
	a

4bd=0

	1		1
(2+a2+		)(2+a2−		)=0
	a		a

	1
a4+4a2+4−		=0
	a2

a⁶+4a⁴+4a²−1=0 p³+4p²+4p−1=0 No i otrzymaliśmy równanie trzeciego stopnia Dalej obliczenia się komplikują Gdybyśmy założyli że np b=0 to mielibyśmy równanie

	1
2+a2+		=0
	a

a³+2a+1=0 a rozwiązanie tego równania też ma pierwiastki w skomplikowanej postaci

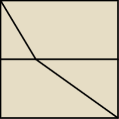
jc: Mariusz, spójrz na takie zadanie. Mamy kwadrat. Idziemy od wierzchołka, do przeciwległego wierzchołka, jednak nasza prędkość w górnej połowie jest dwa razy mniejsza niż w dolnej. W którym miejscu powinniśmy przeciąć poprzeczkę? (możesz przyjąć, że kwadrat ma bok o długości 1, poza tym możesz spróbować rozwiązać zadanie ogólniej, dla ilorazu prędkości = k).

Mariusz: jc chyba trochę przekombinowałeś gdy użyłem modułu sympy do Pythona to otrzymałem pierwiastek postaci −2/(3*(1/2 + sqrt(177)/18)**(1/3)) + (1/2 + sqrt(177)/18)**(1/3) + 2

	2	1		1		√177
x2=−			+3√		+
	3	1   √177   3√ +   2   18		2		18

Bez texa trochę zapis się rozjechał

Mariusz: Na razie doszedłem do czegoś takiego

t2		1	√1+(2−2x)2
	=
t2		2	√1+4x2

Mariusz: s=v₁t₁+2v₁t₂

1		1
	√1+4x2+		√1+(2−2x)2=v1(t1+2t2)
2		2

ale to chyba też chyba do niczego nie doprowadzi,

jc: Mariusz, po prostu wydaje mi się, że rachunek sprowadza się do rozwiązania równania 3 lub 4 stopnia, a Ty masz w tym jesteś dobry.

Mariusz: Nie mam pomysłu na to jak otrzymać to równanie trzeciego bądź czwartego stopnia

	1		1
Całkowita droga którą przejdziemy to		√1+4x2+		√1+(2−2x)2
	2		2

gdzie x to punkt w którym przecinamy poprzeczkę jc Tym zadaniem sprawiłeś mi prezent na zbliżające się urodziny

jc: Zabrakło kilku słów. W którym miejscu powinniśmy przeciąć poprzeczkę, aby podróż trwała najkrócej?

Mariusz: A to teraz wygląda na zadanie optymalizacyjne

	1		1
f(x)=		√1+4x2+		√1+(2−2x)2
	2v1		2v1

Teraz znaleźć minimum tej funkcji ?

jc: Właśnie tak.

Mariusz: Coś chyba jednak jest nie tak w tym rozwiązaniu ponieważ wielomian redukuje się do wielomianu pierwszego stopnia i wychodzi że powinniśmy przeciąć poprzeczkę w połowie

luui: jc, czy chodzi o to zadanie? https://brilliant.org/daily-problems/a-daring-rescue/ (pod Today's Challenge) Problem jest trochę inaczej przedstawiony. Możemy natomiast przenieść turystę 20m w górę oraz zmienić kierunek rwącej rzeki to szukane przecięcie będzie taki samo.

jc: Mariusz, prędkości są różne luui, raczej nie, ale podoba mi zadanie, które wskazałeś. Dziękuję

6latek: Jesli np p=3 i q=−1

	p4		q2
W=		+
	5		6

	34		−12		34		−1
a) W=		+		=		+(		)
	5		6		5		6

czy

	34		(−1)2		3		1
b) W=		+		=		+		?
	6		6		6		6

Prosze tylko o wskazanie ktora odpowiedz .dziekuje

chichi: (b)