 Cześć,
mam takie zadanie:
Cześć,
mam takie zadanie:
| 1 | ||
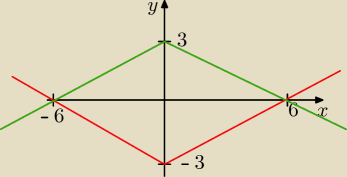
Narysuj figurę okresloną nierównością: | | | + |y| ≤ 3 | |
| 2 |
| 1 | ||
| | | + |y| ≤ 3 | |
| 2 |
| 1 | ||
|y| = 3 − | | | | |
| 2 |
| 1 | 1 | |||
y = 3 − | | | ( na zielono) ∨ y = | | | − 3 ( na czerwono) | ||
| 2 | 2 |
 Mam jeszcze zadanie z prawdopodobienstwa:
W urnie jest 6 bialych kul i 4 czarne. Wyjęto 3 razy po jednej kuli bez zwracania. Oblicz
prawdopodobieństwo, że 3 razy wyjęto kulę białą.
Zrobiłem tak:
Mam jeszcze zadanie z prawdopodobienstwa:
W urnie jest 6 bialych kul i 4 czarne. Wyjęto 3 razy po jednej kuli bez zwracania. Oblicz
prawdopodobieństwo, że 3 razy wyjęto kulę białą.
Zrobiłem tak:
| 6! | 4*5*6 | 120 | ||||
|Ω| = C 36 = | = | = | = 20 | |||
| 1*2*3(6−3)! | 6 | 6 |
| 10! | 8*9*10 | |||
i dalej |Ω| = C310 = | = | = 120 | ||
| 1*2*3(10−3)! | 6 |
| 20 | 1 | |||
P(A) = | = | |||
| 120 | 6 |

| 1 | ||
P(A) czyli | ||
| 6 |
| 120 | 1 | |||
P(A) = | = | |||
| 720 | 6 |


| 1 | 1 | |||
czyli po prostu bedzie y = | | | + 3 ∧ y = | | | − 3 ? | ||
| 2 | 2 |
| 1 | ||
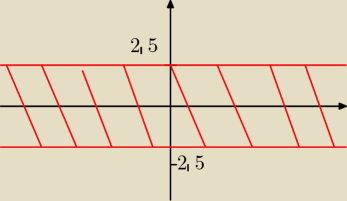
|y| ≤ 3 − | ||
| 2 |
| 1 | ||
y≥ −3 + | = −2,5 | |
| 2 |
 pole ograniczone 2 prostymi
pole ograniczone 2 prostymi

| 1 | ||
przy | powinien stać x | |
| 2 |
| 1 | ||
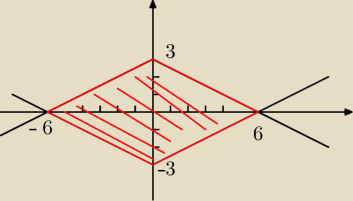
czyli jest tak: | | x| + |y| ≤ 3 czy to coś zmienia ? | |
| 2 |


| 1 | ||
|y| ≤ 3 − | | x| | |
| 2 |
| 1 | 1 | |||
y≤3 − | | x| i y≥ − 3 + | | x| | ||
| 2 | 2 |
| 1 | 1 | |||
y≤3+ | x y≥ − 3 − | x | ||
| 2 | 2 |
| 1 | 1 | |||
y≤3− | x y≥ − 3 + | x | ||
| 2 | 2 |



 zet możesz zerknąć jeszcze raz na to zadanie z prawdopodobieństwa? Bo wyszło na to, że nie
zależnie z jakiego wzoru skorzystam wynik jest ten sam w obu przypadkach. Chociaż wariacje bez
powtórzeń w tym zadaniu byłyby wskazane...
Dziękuję wam za odpowiedzi
zet możesz zerknąć jeszcze raz na to zadanie z prawdopodobieństwa? Bo wyszło na to, że nie
zależnie z jakiego wzoru skorzystam wynik jest ten sam w obu przypadkach. Chociaż wariacje bez
powtórzeń w tym zadaniu byłyby wskazane...
Dziękuję wam za odpowiedzi  macie jakiś pomysł na to ostatnie zadanie? tam trzeba będzie chyba wykorzystać wzór na pole i
objetość stożka....
macie jakiś pomysł na to ostatnie zadanie? tam trzeba będzie chyba wykorzystać wzór na pole i
objetość stożka....
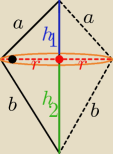 Ta bryła , to dwa stożki sklejone podstawami
Ta bryła , to dwa stożki sklejone podstawami  h1+h2= c
V(br) = 13πr2*h1+ 13πr2*h2=13πr2( h1+h2)
V(br)= 13πr2*c
Pc( br) = Pb( st. I)+Pb(st. II)=πra + πrb= πr( a+b)
a, b −− dł. tworzących stożków
powodzenia ....
h1+h2= c
V(br) = 13πr2*h1+ 13πr2*h2=13πr2( h1+h2)
V(br)= 13πr2*c
Pc( br) = Pb( st. I)+Pb(st. II)=πra + πrb= πr( a+b)
a, b −− dł. tworzących stożków
powodzenia ....
 zet prosze Cie zobacz jeszcze raz to zadanie z prawdopodobieństwa... Mozliwe jest aby
korzystając z dwóch róznych wzorów wyszedł ten sam wynik. Tzn. no bo faktycznie w tym zadaniu
należało skorzystć z wariacji, ale w efekcie końcowym wyszło to samo co ze wzoru na
prawdopodobieństwo... i nie wiem juz o co chodzi
zet prosze Cie zobacz jeszcze raz to zadanie z prawdopodobieństwa... Mozliwe jest aby
korzystając z dwóch róznych wzorów wyszedł ten sam wynik. Tzn. no bo faktycznie w tym zadaniu
należało skorzystć z wariacji, ale w efekcie końcowym wyszło to samo co ze wzoru na
prawdopodobieństwo... i nie wiem juz o co chodzi

| n! | n! | |||
Vnk= | = k!*Cnk = k!* | |||
| (n−k)! | k!*(n−k)! |
 mam jeszcze jedno pytanie.... a w zasadzie dwa dotyczące ostatniego zadania
mam jeszcze jedno pytanie.... a w zasadzie dwa dotyczące ostatniego zadania  dlaczego kiedy obliczasz pole, korzystasz ze wzoru na Pb = πrl, a nie z tego wzoru:
P = πr(r+l)?
podane pole i objetośc to jest już odpowiedź? no bo w sumie chyba z takich danych jakie mamy
nie da się już nic wiecej wykrzesać....
dlaczego kiedy obliczasz pole, korzystasz ze wzoru na Pb = πrl, a nie z tego wzoru:
P = πr(r+l)?
podane pole i objetośc to jest już odpowiedź? no bo w sumie chyba z takich danych jakie mamy
nie da się już nic wiecej wykrzesać....
 Dlatego, pole całkowite takiej bryły to suma pól bocznych obydwu stożków.
zadanie należy jeszcze dokończyć
odp. ma być podana tylko w zależności od danych a i b
c= a2+b2 => c = √a2+b2
Dlatego, pole całkowite takiej bryły to suma pól bocznych obydwu stożków.
zadanie należy jeszcze dokończyć
odp. ma być podana tylko w zależności od danych a i b
c= a2+b2 => c = √a2+b2
| a*b | ||
r= | ||
| c |
| a2*b2 | ||
r2= | ||
| a2+b2 |

 Ale za to chłopak pracowity , więc należy Mu pomagać
Ale za to chłopak pracowity , więc należy Mu pomagać 
 Pozdrawiam
Pozdrawiam 
 spokojnie, spokojnie, z dnia na dzien idzie mi coraz lepiej
spokojnie, spokojnie, z dnia na dzien idzie mi coraz lepiej  dziekuje wam i dobranoc
dziekuje wam i dobranoc 
 P.S. mam nadzieje że nauki nie idą w las
P.S. mam nadzieje że nauki nie idą w las 
