| 1 | ||
|BC|. Oblicz tangens kąta PAB. Czy ktoś pokazałby mi jak rozwiązać takie zadanie? | ||
| 4 |
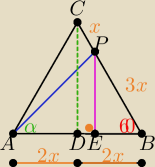Niech a=4x, x>0
| 3 | 3√3 | |||
|EB|= | x, |PE|= | x | ||
| 2 | 2 |
| 3 | 1 | |||
|DE|=|DB|−|EB| ⇒ |DE|=2x− | x ⇒ |DE|= | x | ||
| 2 | 2 |
| 1 | 5 | |||
|AE|=|AD|+|DE| ⇒ |AE|=2x+ | x ⇒ |AE|= | x | ||
| 2 | 2 |
| |PE| | 3√32x | 3√3 | ||||
tg(α)= | ⇒ tg(α)= | ⇒ tg(α)= | ||||
| |AE| | 52x | 5 |
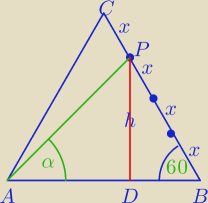
| 3x√3 | ||
h= | ||
| 2 |
| 3x | ||
|DB|= | ||
| 2 |
| 3x | 5x | |||
|AD|=4x− | = | |||
| 2 | 2 |
| h |
| |||||||||
tgα= | = | |||||||||
| |AD| |
|
| 3√3 | ||
tgα= | ||
| 5 |
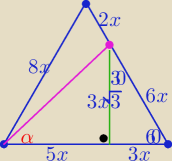
| 3x√3 | 3√3 | |||
tgα= | = | |||
| 5x | 5 |