równoległobok
Lidka:
Dostałam od Pana takie zadanie
W równoległoboku ABCD o kącie rozwartym 120 stopni
Środkiem boku AD jest punkt E, a punkt F dzieli bok AB w stosunku 2:1
licząc od wierzchołka A
Odcinki CE i DF przecinaja się w punkcie G
Jaką część pola równoległoboku ABCD stanowi pole czworokąta AEGF
Mogę liczyć na pomoc, bo nic mi nie chce wyjść
9 gru 21:13
chichi: Pokaż Lidka co tam wystrugałaś
9 gru 21:44
Eta:
9 gru 22:30
9 gru 23:11
Allan:
jest inny wynik
10 gru 00:06
Eta:
A jaki ?
10 gru 00:21
Eta:
Sprawdziłam .... i nie chce być inny
10 gru 00:26
Allan:
wynik to 5/24
10 gru 00:45
chichi: @
Eta Potwierdzam twój wynik
10 gru 01:13
Eta:
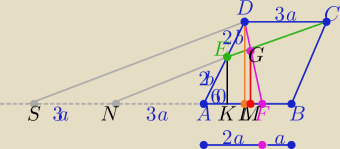
Moje oznaczenia są takie jak na rys:
|EK|=b
√3 , |DL|=2b
√3
ΔSDF ∼ΔNGF
| | 8a | | DL | | 5b√3 | |
to |
| = |
| ⇒ |GM|= |
| |
| | 5a | | GM | | 4 | |
P(AEGF)= P(ΔNGF)−P(ΔANE)
| | 25ab√3 | | 12ab√3 | | 13ab√3 | |
P(AEGF)= |
| − |
| = |
| |
| | 8 | | 8 | | 8 | |
P(ABCD)= 6ab
√3
=====
10 gru 01:14
Bogdan:
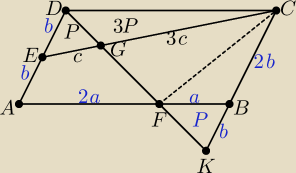
Szkic innego rozwiązania. △KCG∼△EGD w skali k = 3 (do uzasadnienia), stąd |GC| = 3|EG|.
Pole równoległoboku ABCD = P
R
| | 1 | |
oraz pola trójkątów: PEGD = PFBK = P, PGCD = 3P i PECD = 4P = |
| PR |
| | 4 | |
| | 1 | | 1 | |
PEGD = P = |
| PR, PAFD = |
| PR. |
| | 16 | | 3 | |
| | 1 | | 1 | | 13 | |
Pole czworokąta PAEFG = PAFD − PEGD = |
| PR − |
| PR = |
| P R. |
| | 3 | | 16 | | 48 | |
10 gru 14:29
Eta:
10 gru 14:30