Skąd to zadanie Saizou : Dzień dobry, ma pytanie, czy ktoś z Was wie skąd pochodzi zadanie poniżej: W ostrosłupie prawidłowym czworokątnym krawędź boczna ma długość b, a dwie sąsiednie krawędzie boczne tworzą kąt α. Oblicz pole P przekroju tego ostrosłupa płaszczyzną, która zawiera przekątną podstawy i jest prostopadła do krawędzi bocznej ostrosłupa. Z góry dziękuję. Chętnych zapraszam do rozwiązania

Filip: oho, Saizou wrocil na forum z zadaniem ze stereometri, w takim razie musi byc jakis haczyk

Saizou : Nie ma haczyka. Po prostu bardzo fajne zadanko mi wpadło w ręce i chciałbym wiedzieć skąd ono jest. PS. Ja tu zaglądam co jakiś czas tylko się nie udzielam

Filip: Zadanie jest żmudne ze wzgledu na obliczenia. Podam mniej wiecej rozwiazanie i sprawdzisz czy okej bo niestety stereometrii dawno nie robilem 1) Z twierdzenia sinusow obliczamy dlugosc krawedzi podstawy 2) Nastepnie wyznaczamy dlugosc przekatnej szescianu 3) Wyznaczamy dlugosc wysokosci ostroslupa z twierdzenia pitagorasa

	a√2
(H2 + (		)2 = b2)
	2

Wysokosc naszego przekroju iobliczymy z trojkatow podobnych No i pole to formalnosc, oczywiscie trojkaty podobne sa, ale nie wiem za bardzo jak tu rysowac

Słoniątko: zadanie pochodzi z książki wydanej ponad 15 lat temu, ale nie pamiętam tytułu niestety, spróbuję sobie przypomnieć jeszcze

Saizou : Długość przekątnej sześcian

Eta:

	h2*a2
P2=
	2

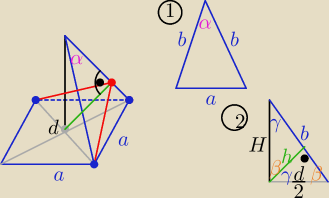
z 1/ z tw. cosinusów : a²=2b²(1−cosα)

	H*d		a2H2
z 2/ h=		h2=
	2b		2b2

	a2		2b2−a2
i z tw. Pitagorasa H2=b2−		=
	2		2

i teraz dokończ..........

Saizou : Eta liczyłem tak samo