Trygonometria z parametrem Zekken7294: Dla jakich wartości parametru m równanie sin⁴x+cos⁴x=m²−3 ma rozwiązanie? Robie dwoma różnymi sposobami i wychodzą dwa różne wyniki, prosiłbym o pomoc, które z nich jest błędne i co jest nie tak. I sposób sin⁴x+(cos²x)²=m²−3 sin⁴x+1−2sin²x+sin⁴x=m²−3 2sin⁴x−2sin²x−m²+4=0 niech t=sin²x i t∊<0;1> 2t²−2t−m²+4=0 rozwiązuje warunki Δ≥0 i t∊<0;1> z czego wychodzi ze m<−√7/2 i m>√7/2 II sposób sin⁴x+cos⁴x przekształcam do 1−1/2sin²2x po czym wychodzi ze m∊<−2;−√7/2>∪<√7/2;2> W którym rozumowaniu jest błąd?

Filip: (1−2sin²x)² = 1 − 4sinx + 4sin²x

Filip: 1 − 4sin²x + 4sin⁴x

Filip: stop, przeczytalem cos(2x)

Zekken7294: jak już się tutaj rozpisałem to sam znalazłem, drugie rozumowanie dobre. w pierwszym warunki zle bo dalem t tak jakby bylo tylko jedno miejsce zerowe...

ICSP: W którym miejscu uwzględniasz warunek t ∊ [0,1] z pierwszego sposobu rozwiązania?

ABC:

	1
musi zachodzić		≤m2−3≤1
	2

	7
czyli		≤m2≤4
	2

czyli II rozumowanie jest poprawne

Zekken7294: stwierdzilem ze wierzcholek paraboli ma byc w <0;1> tak jakbym brał pod uwagę tylko Δ=0. Coś mózg mi się zawiesił

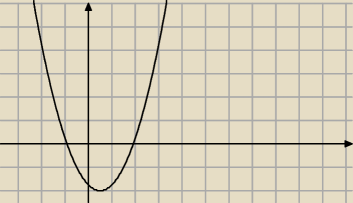
ICSP: wierzchołek należy do [0;1], ale brak pierwiastków w tym przedziale.

Filip: @ABC z tego co napisales, to czy wyrazenie sin^xα + cos^xα, gdzie x ∊ N₊ najwieksza wartoscia jaka przyjmuje to 1?

ICSP: Dla x ≥ 2 Dla x = 1 największa wartość to √2

Filip: Ok, dzieki A z wartoscia najmniejsza tego wyrazenia to jak jest?