Zadanie na dowodzenie Alaias: W kwadracie ABCD punkt E dzieli bok BC w stosunku 2:1 licząc od punktu C, odcinek AE przecina przekątną DB w punkcieE. Wykaż, że pole czworokąta DFEC stanowi 11/24 pola kwadratu ABCD.

Alaias: Przecina przekątną w punkcie F

Alaias:

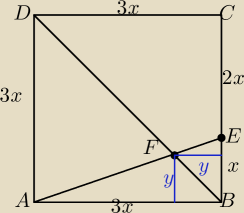
a7: ΔADF jest podobny do ΔEBD w skali 3 czyli PΔADF=9*PΔAEB 1/2*3x*(3x−y)=1/2*9*xy 9x²−3xy=9xy 9x²=12xy y=3/4x PΔABF=1/2*3x*y= P_DFEC=P_ABCD−P{ADF}−P_EFB−P{AFB}=...... dalej sama, dasz radę?

chichi: ΔADF jest podobny do ΔEBD ? ? ? ?

a7: EBF oczywiście

a7: ojej jeszcze raz, jakieś literówki

a7: trójkąt ADF jest podobny do trójkąta BEF (cecha kkk) w skali 3, czyli stosunek ich pól będzie równy 9 P_ADF=9P_BEF 1/2 3x*(3x−y)=1/2*9*xy ⇒ y=3/4x P_ABF=..... P_DFEC=

Alaias: Dzięki

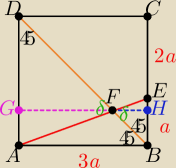chichi: |CE|=2a, |EB|=a ⇒ |CB|=3a, |∡ADB|=|∡FBE|=45, |∡DFA|=|∡EFB|=δ (kąty wierzchołkowe),

	a		1
|∡DAF|=|∡FEB| (kąty naprzemianległe), zatem ΔEFB~ΔAFD (cecha k−k−k) w skali k=		=
	3a		3

	1		1		9
niech |GF|=h ⇒ |FH|=		h oraz |GF|+|FH|=3a=h+		h ⇒ h=		a
	3		3		4

	1		9		27
PΔAFD=		*3a*		a=		a2
	2		4		8

	1		3
PΔABE=		*3a*a=		a2
	2		2

	27		3		33
PDFEC = PABCD − PΔAFD − PΔABE = (3a)2 −		a2 −		a2 =		a2
	8		2		8

PDFEC		338a		11
	=		=
PABCD		9a		24

Q.E.D.

chichi: @a7 P_ΔAFB + P_ΔEFB = P_ΔABE który jest prostokątny i od razu mamy jego pole

chichi: W stosunku tylko zjadłem ², ale to i tak ulega skróceniu

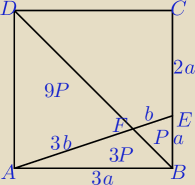Bogdan: Inne rozwiązanie, szkic: △AFD∼△BEF w skali k = 3, pola P_BEF = P i P_AFD = k²*P = 9P oraz P_ABF = 3P, P_ABE = 4P ⇒ P_ABCD = 6*4P = 24P

	PDFEC		11
PDFEC = 24P − (9P + 3P + P) = 11P zatem		=
	PABCD		24

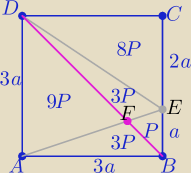Eta: W trapezie ABED : P(trapezu)= 16P P(DCEF)=11, P(ABCD)=24P

P(DCEF)		11
	=
P(ABCD)		24