| 1 | 1 | |||
f(x)=√(sinx− | ) (sinx+√3/2) + ln(cosx) to cale wyraznie (sinx− | ) (sinx+√3/2) | ||
| 2 | 2 |
| 1 | 1 | |||
i ja chcialam tak sin≥ | ⋀sinx≥−√3/2) ⋀ cox>0 lub sin≤ | ⋀sinx≤−√3/2) ⋀ cox>0 | ||
| 2 | 2 |
 f(x)=√(sinx−12)*(sinx+√32)
sinx=t, −1≤ t≤1
f(t)=√(t−12)*(t+√32)
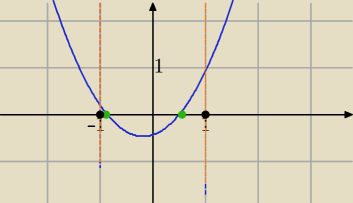
(t−12)*(t+√32)≥0 parabola skierowana do góry
f(x)=√(sinx−12)*(sinx+√32)
sinx=t, −1≤ t≤1
f(t)=√(t−12)*(t+√32)
(t−12)*(t+√32)≥0 parabola skierowana do góry
| −√3 | 1 | |||
−1≤t≤ | lub | ≤t≤1 | ||
| 2 | 2 |
| −√3 | 1 | |||
−1≤sinx≤ | lub | ≤sinx≤1 | ||
| 2 | 2 |
| −√3 | 1 | |||
−1≤t≤ | lub | ≤t≤1⇔ | ||
| 2 | 2 |
| −√3 | 1 | |||
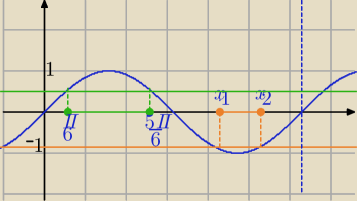
−1≤sinx≤ | lub | ≤sinx≤1⇔ | ||
| 2 | 2 |
| π | 5π | 4π | 5π | |||||
x ∊< | , | > lub x∊< | , | > | ||||
| 6 | 6 | 3 | 3 |