funkcje wymierne green: Witam. Bardzo proszę o pomoc w rozwiązaniu zadań.Jeśli można to krok po kroku abym zrozumiała jego wykonanie . Dziękuję. Wykres funkcji f(x)=−2x przesunięto o wektor (2;−4) i otrzymano wykres funkcji g(x). Napisz: −wzór tej funkcji −naszkicuj jej wykres −podaj równanie asymptot −wyznacz dziedzinę −zbiór wartości −wyznacz dla jakich argumentów funkcja przyjmuje wartośc dodatnią

6latek: To nie jest funkcja wymierna

	ax+b
Funkcja wymierna jest postaci y=
	cx+d

f(x)=−2x to funkcja liniowa

6latek: Chyba ze wzor to

	−2
y=
	x

Ale to musisz wyjasnic

jc: 6latku, to jest funkcja wymierna. Funkcja wymierna = iloraz wielomianów (w mianowniku wielomian niezerowy). −2x = (−2x)/1 −2x jest wielomianem, 1 jest wielomianem niezerowym Przy okazji, teraz lepszą nazwą wydaje mi się określenie − wyrażenie wymierne (funkcja wymierna może nie być funkcją).

6latek: Dzien dobry jc. Pozdrawiam Ja tak wlasnie zastanawialem sie nad tym zapisem (−2x)/1 Tylko potem jej warunki np asymtoty ,dziedzina zbior wartosci wiec pomyslaem o takim wzorze

jc: Dzień dobry, spojrzałem do angielskiej wik, jednak funkcje wymierne (wolę najbardziej rozpowszechnione określenia, matematyka i tak jest trudna).

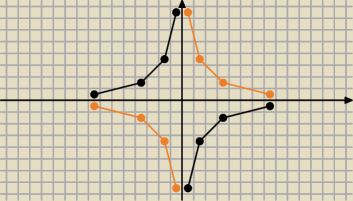
green: Jeśli dobrze zrozumiałam to powinno być: Dziedzina funkcji to x∊R\ (0) x −4 −2 −1 −1/2 1/2 1 2 4 y=−2/x 1/2 1 2 4 −4 −2 −1 −1/2 Funkcje mają II osie symetrii, to: y=−2/x i y=2/x. Rysunki powyżej (czarny to g(x)=−2/x a pomarańcz f(x)=2/x Własności funkcji: −dla x < 0 funkcje y przyjmuje wartości dodatnie x > 0 przyjmuje wartości ujemne −funkcja g nie posiada miejsc 0 −funkcja y jest rosnąca w przedziałach(−∞;0) i (0;∞) ale nie jest rosnąca w swojej dziedzinie −prosta y=0 jest asymptotą poziomą prosta x=0 jest asymptotą pionową funkcji g

6latek:

	−2
f(x)=
	x

Taki jest wzor funkcji f(x)? Tak Teraz zauwaz ze oni nie pytaja Ciebie o f(x) tylko o g(x) Funkcja g(x) powstaje przez przesuniecie f(x) o wektor [2,−4]

	−2
wiec g(x)=		−4
	x−2

	−2
wiec f(x) =		przesuwasz o 2 jednostki w prawo po osi OX
	x

Nastepnie otrzymany wykres przesuwasz o 4 jednostki w dol i masz wtedy g(x) Prosze aby ktos jeszcze sprawdzil

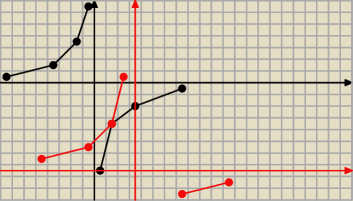
green: i jeszcze przesunięcie o wektor (2;−4) y=−2/x niestety cały wykres się nie zmieścił ale analogicznie jak w poprzednim.

green: ok,rozumiem czyli powyższe przesunięcia będą dobre

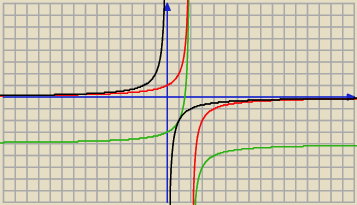
6latek: Narysuje Ci tutaj w programie

	−2
y=		czarny
	x

	−2
y=		czerwony
	x−2

	−2
y=		−4 zielony
	x−2

green: Rozumiem,wszystko po kolei najpierw rysuję wykres czarny" podstawowy", potem czerwony przesuwam o 2 jednostki w prawo a na końcu o 4 w dół zielony

6latek: Tak

	−2		1
Teraz zastanow sie jakbys narysowal wykres y=		znajac podstawowy wykres y=		?
	x		x

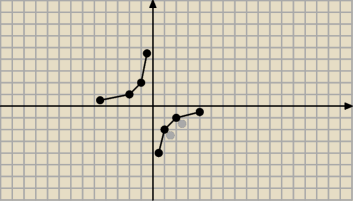
green: y=−2/x x −4 −2 −1 −1/2 1/2 1 2 4 y=−2/x 1/2 1 2 4 −4 −2 −1 −1/2

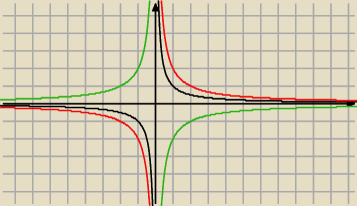
6latek: Pokaze na wykresach

	1
y=		czarny ten wykres znasz
	x

	2
y=		czerwony rysujesz
	x

Rysujesz go tak Zwiekszasz x_y dwa razy a wartosci funkcji pozostaja te same przyklad

	1		1
y=		dla x=2 y=
	x		2

	2		2		1
teraz y=		x=4 to y=		=
	x		4		2

	−2
Teraz wykres czerwony odbijasz symetrycznie wzgledem osi OY i masz wykres zielony y=
	x

Qulka:

6latek: Dobry wieczor Zdrowa jestes? Moja ciocia (80 lat) ma tego wirusa , ale juz dochodzi do siebie

green: To brat ,już lepiej ale 1,5 miesiąca przechorowane w tym szpital. Małe zmiany w płucach i podwyższone czynniki wątrobowe. Za miesiąc kontrolne CT i morfologia. Cały czas osłabienie i problemy z koncentracja.

Qulka: 6latek wszystko ok .. znów w szkole więc obłęd od września straszny

6latek: To sie ciesze. Musimy dbac o siebie w tym czasie . Ja na swieta zostane sam .Corki nie przyjada . Dobrze ze jest internet to bedzie mozna porozmawiac . Trzymaj sie zdrowo .