rozwiązać równanie:

rozwiązać równanie: jaros: Dobry wieczór, mam takie równanko do rozwiązania emotka

	π
arctg3^x −arctg3^−x =
	6

2 gru 19:21

Jerzy: Daruj sobie ten uśmieszek,nawet nie potrafisz podziękować za pomoc.Dla mnie spadasz.

2 gru 20:00

Jeszcze student: Spróbuj może zrobić graficznie; Przyjmij 3^x = t, t>0; I masz arctg(t) = pi/6 + arctg(1/t)

2 gru 20:11

Morwa biała : Jerzy Przyjmij ze chlopak zrozumial w koncu ta dziedzine i byl tak szczesliwy ze zapomnial .

2 gru 20:16

jaros: No dokładnie tak jak piszę @Morwa biała, przygotowuje się na jutrzejsze minikolokwium z tego i zapominałem porostu, bo od razu liczyłem inne przykłady. Oczywiście dziękuje za pomoc przy tamtym przykładzie.

2 gru 21:05

jaros: Ojjj, a algebraicznie by nie poszło?

2 gru 21:05

jc:

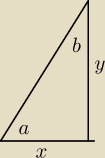
arctg y/x = a, arctg x/y = b, a+b=π/2 W zadaniu x/y = t > 0. arctg t + arctg 1/t = π/2.

2 gru 21:19

Morwa biała : arc tg(x)−arctg(y)=

	x−y
1)arc tg		dla xy>−1
	1+x*y

	x−y
2) dla x>0 i xy<−1 = π+arc tg
	1+xy

	x−y
3) dla x<0 xy<−1 = −π+arctg
	1+xy

2 gru 21:26

kerajs: Gdyby obie strony potraktować tangensem i zastosować wzór na tangens różnicy do dostanie się:

3^x−3^−x		π
	=tg
1+3^x3^−x		6

a to jest równaniem kwadratowym względem 3^x.

2 gru 22:08

kerajs:

2 gru 22:09

Mila: arctg3^x=α

	1		π
arctg		=β i α,β∊(0,		)
	3^x		2

	π		1		π
α+β=		bo arctg(t)+arctg(		)=		dla t>0 ( patrz 21:19 )
	2		t		2

	π		4π
α−β=		⇔2α=
	6		6

	2π		π		π
α=		=		i β=
	6		3		6

	π		1
arctg(3^x)=		⇔3^x=√3⇔x=
	3		2

	1		π		1		1
arctg		=		⇔		=
	3^x		6		3^x		√3

	1
x=
	2

	1
odp. x=
	2

========

2 gru 22:30

jaros: Dziękuje ślicznie @mia i wszystkim którzy pomagali emotka

a takie jeszcze szybkie pytano to co @jc napisał w 21:19 można sodować np tutaj?

	π
arcsin(1 − 𝑥) − 2arcsin𝑥 =
	2

3 gru 00:40

Morwa biała : Skanuje Tobie material wiec czekaj (ale troche zejdzie wiec rano moze sobie zobaczysz

3 gru 01:32

Morwa biała : https://zapodaj.net/2d44954b69104.jpg.html https://zapodaj.net/2c8782229089c.jpg.html https://zapodaj.net/41cef5a71c5c5.jpg.html https://zapodaj.net/9037ad6745da6.jpg.html https://zapodaj.net/acdeba33ac3d5.jpg.html Reszta wnastepnym poscie

3 gru 01:43

Morwa biała : https://zapodaj.net/f245020c70057.jpg.html https://zapodaj.net/31c8b1c3e9e4a.jpg.html https://zapodaj.net/26de8fafbd6fd.jpg.html https://zapodaj.net/0a5a4299b4841.jpg.html https://zapodaj.net/7b3c696a0d6f9.jpg.html Wybierz co Ci potrzeba

3 gru 01:46

Morwa biała : https://zapodaj.net/1aeb9867b6583.jpg.html To jest brakujaca strona 108−109 Nie wiem dlaczego jej braklo .

3 gru 02:09

jaros: A gdyby Pani jeszcze była, kiedy obie strony można w funkcjach cyklometrycznych traktować sinsuem, cos, tangensem i ctg? Znaczy tak się da rozwiązać każde równanie?

3 gru 02:19