Geometria analityczna Sotomski: Dane są proste zawierające dwa boki równoległoboku y=−x−1, y=2x−4. Punkt A(1,7), jest jednym z wierzchołków równoległoboku. Oblicz współrzędne pozostałych wierzchołków. Jedyne co obliczyłem to punkt przecięcia się prostych S(−1,2) oraz współrzędną wierzchołka C(1,−11). Nie wiem co mam dalej zrobić

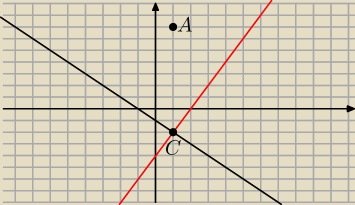
Morwa biała : uwaga nr 1 Masz w zadniu podane w tych prostych zawieraja sie dwa boki wiec punkt przeciecia sie tych prostych to jest jeden z wierzcholkow tego rownolegloboku ( anie punkt przciecia przekatnych ) uwaga nr 2 nalezy zawsze zrobic rysunek 3) Wiemy ze w rownolegloboku przeciwlegle boki sa rownolegle a) piszesz rownanie prostej ronoleglej do y=−x−1 i przechodzacej przez A (punkt przeciecia tej prostej z prosta y=2x−4 da wierzcholek np B To samo robisz z druga prosta

Morwa biała : Musisz porosic a@b zeby drugi raz wpisala Ci rozwiazanie Natomiast ja bede nietety musial opuscic to foru zeby nie razac siebie i innych uzytkownikow forum na takie dzialanie jak poprzednio tutaj

Sotomski: Dalej mi nic nie wychodzi

Jeszcze student: Masz punkt A(1,7) Zauważ, że punkt ten nie należy do żadnej z tych prostych. Czyli pozostałe 3 będą zawierały się w jakiejś prostej. Punkt przecięcia prostych − przeciwległy wierzchołek D (−1;2). Masz do znalezienia jeszcze 2 punkty o współrzędnych (xb, −xb−1) i drugi (xc;2xc−4) Masz dwa wektory, które są takie same AC i BD. Rozpisz równość AC = BD i wyjdzie

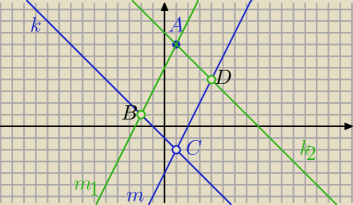
Mila: A=(1,7) k: y=−x−1, m: y=2x−4 1) C− punkt przecięcia prostych ki m −x−1=2x−4 3x=3, x=1 i y=−2 C=(1,−2) 2) Prosta równoległa do m i przechodząca przez A m₁: y=2x+b i A∊m₁ 7=2*1+b, b=5 m₁: y=2x+5 Punkt przecięcia prostej m₁ i prostej k: −x−1=2x+5 3x=−6 x=−2 i y=1 B=(−2,1) 3) prosta równoległa do k i przechodząca przez A: k₁: y=−x+b i A∊k₁ 7=−1+b, b=8 k₁: y=−x+8 Punkt przecięcia prostych k₁ i m 2x−4=−x+8 3x=12 x=4 i y=4 D=(4,4) =====