Logarytmy
jaros: Która z liczb jest większa log2𝑎 czy log3𝑎? Tzn. jak cos takiego udowodnić?
2 gru 16:15
ICSP: Zależy od a.
2 gru 16:20
Jerzy:
Jakaś bzdura. Np. log21 = log31
2 gru 16:23
jaros: Znaczy tu nieważne co podstawie za a w równości logarytmicznej log2a = log3a to będzie 2 = 3
więc zawsze log3𝑎 z wyjątkiem 1
2 gru 16:57
jaros: No i można jeszcze tylko dziedzinę wyliczyć dla a
2 gru 16:57
Filip:
to ciekawe, ze wedlug ciebie log
33 > log
23

2 gru 17:02
jaros: No ale to prwada przeciez 1 > 0,62353
2 gru 17:17
jaros: A nie ważne, kalkulator zwariował i ja również
2 gru 17:18
Morwa biała :
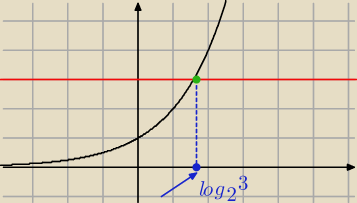
Wytlumaczylbym sobie tak
log
ab=c to a
c=b to z definicji
przyklad log
33=1 bo 3
1=3
log
23≈1,58 bo 2 nalezy podniesc do potegi wiekszej niz jeden zeny dostac 3
Np log
2 z 3 mozesz odczytac tak
Zrobilem ci rysunek
1) Rysujesz na papierze milimetrowym wykres funkcji y=2
x
2) na tym samym wykresie rysujesz y=3
3) punkt przeciacia sie wykresow rzutujesz na os OX i na osi odczytujesz wynik w przyblizeniu
Tak jednak sie robilo gdy nie bylo maszyn liczacych
Teraz te wartosci mozesz odczytac bardzo szybko np na klakulatorze .
2 gru 17:27

 Wytlumaczylbym sobie tak
logab=c to ac=b to z definicji
przyklad log33=1 bo 31=3
log23≈1,58 bo 2 nalezy podniesc do potegi wiekszej niz jeden zeny dostac 3
Np log2 z 3 mozesz odczytac tak
Zrobilem ci rysunek
1) Rysujesz na papierze milimetrowym wykres funkcji y=2x
2) na tym samym wykresie rysujesz y=3
3) punkt przeciacia sie wykresow rzutujesz na os OX i na osi odczytujesz wynik w przyblizeniu
Tak jednak sie robilo gdy nie bylo maszyn liczacych
Teraz te wartosci mozesz odczytac bardzo szybko np na klakulatorze .
Wytlumaczylbym sobie tak
logab=c to ac=b to z definicji
przyklad log33=1 bo 31=3
log23≈1,58 bo 2 nalezy podniesc do potegi wiekszej niz jeden zeny dostac 3
Np log2 z 3 mozesz odczytac tak
Zrobilem ci rysunek
1) Rysujesz na papierze milimetrowym wykres funkcji y=2x
2) na tym samym wykresie rysujesz y=3
3) punkt przeciacia sie wykresow rzutujesz na os OX i na osi odczytujesz wynik w przyblizeniu
Tak jednak sie robilo gdy nie bylo maszyn liczacych
Teraz te wartosci mozesz odczytac bardzo szybko np na klakulatorze .