Rozwiązać nierówność tomek123098: Rozwiąż nierówność √5−x > x + 1 1) Najpierw wyznaczyłem dziedzinę x ∊ (−∞, 5> 2)Równanie podzieliłem sobie na dwa przedziały x ∊ (−∞, 1) − czyli kiedy liczba po prawej stronie jest ujemna x ∊ <1, 5> − czyli kiedy liczba po prawej stronie jest ujemna 3) Teraz obie strone podnoszę do kwadratu i kolejno dla pierwszego przedziału wygląda to następująco: 5 − x > x² + 2x + 1 x² +3x − 4 < 0 Zaś dla drugiego przydziału to samo tylko z odwronym znakiem x² +3x − 4 > 0 Dla obu równań x₁ = 1 x₂ = −4 4) Z pierwszego przedziału otrzymuję rozwiązanie x ∊ <−1, 1) Z drugiego przedziału x ∊ (−∞, −4) Rozwiązaniem jest suma tych dwóch przedziałów, jest to rozwiązanie błędne, gdzie popełniłem błąd?

Jerzy: Jeśli prawa jest ujemna, czyli x + 1 < 0 ⇔ x < −1 , to każda liczba z przedziału (−∞ ,−1) spełnia nierówność

Jerzy: A ty twierdzisz,że prawa strona jest ujemna dla x ∊ ( − ∞,1) oraz jest ujemna dla x ∊ <1,5>

Eta: Najprostsza metoda przez podstawienie x≤5 i √5−x=t, t≥0 ⇒ 5−x=t² ⇒ x= 5−t² i mamy t>5−t²+1 i t≥0 (t+3)(t−2)>0 i t≥0 ⇒ t>2 to 5−x>4 i x≤5 Odp: x< 1 =======

Jerzy: Polemizowałbym, że to najprostsza Pierwszy przedział rozwiązań: (−∞,−1) Drugi przedział (−4,1) Ich suma: (−∞,−1) U (−4,1) = (−∞,1) i "po ptokach", jak niektórzy na tym forum lubią mawiać

tomek123098: Jerzy, źle przepisałem to jak to robiłem, wykonywałem za to całe zadanie z przedziałami x ∊ (−∞, −1) oraz x ∊(−1, 5> i otrzymałem taki wynik jak napisałem Tak więc gdzie popełniłem błąd? Dzięki Eta za metodę

Eta:

Jerzy: Dla x + 1 < 0 ⇔ x < −1 każde liczba z przedziału (−∞,−1) jest rozwiazaniem Drugi przedział , to (−4 ,1) , a ich suma to (−∞,1)

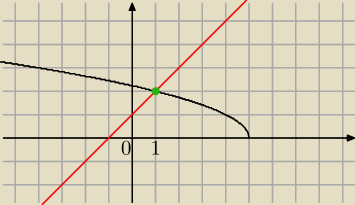
6latek : Z wykresu funkcji y=√x po przeksztalceniach rysujemy wykres y=√5−x y=x+1 znany Widzimy ze x∊(−∞,1)

tomek123098: Dobra napisze to jeszcze raz jak robiłem to krok po kroku. 1) Najpierw pierwszy przedział x ∊ <−1, 5> czyli wtedy kiedy możemy podnieść obie strony do kwadratu bez zmiany znaku. 5 − x > x² + 2x + 1 x² + 3x − 4 < 0 Rozwiązanie tego równania to x ∊ (−4, 1) jednak my musimy wziąć rozwiązanie tylko dla x ∊ <−1, 5> (bo robimy dla tego przedziału, więc ostateczne rozwiązanie z pierwszego przedziały to x ∊ <−1, 1) 2) Teraz drugi przedział x ∊ (−∞, −1) czyli wtedy kiedy zmieniamy znak przy podnoszeniu stron do kwadratu. 5 − x < x² + 2x + 1 x² + 3x − 4 > 0 Rozwiązanie tego równania to x ∊ (−∞, −4) U (1, ∞) jednak my musimy wziąć rozwiązanie tylko dla x ∊ (−∞, −1), bo robimy dla tego przedziału, więc ostateczne rozwiązanie z drugiego przedziały to x ∊ (−∞, −4) Co robię nie tak?

tomek123098: Ja wiem jak zrobić to na inne sposoby jak metodą graficzną lub przez podstawienie tego t, ale chcę wiedzieć co ja zrobiłem nie tak w swojej metodzie, gdzie jest błąd?

ICSP: Podnosić do kwadratu możesz tylko i wyłącznie kiedy obie strony są tego samego znaku.

tomek123098: No i dzięki, sprawa wyjaśniona

Jerzy: 14:47 , no to sprawdzamy , np: − 3 < − 2 (−3)² < (−2)² 9 < 4 , sprzeczność

ICSP: Przecież to oczywiste, że przy ujemnych liczbach należy zmienić znak. Chodziło mi o to, że jeżeli liczby mają różny znak to nie ma reguły na to co nam wyjdzie po podniesieniu.

Jerzy: Dla ciebie tak, ale dla ucznia nie zawsze. Lepiej napisać: "gdy obydwie strony są nieujemne".