powierzchnia boczna walca obrotowego po rozwinięciu jest prostokątem , którego p żabcia: powierzchnia boczna walca obrotowego po rozwinięciu jest prostokątem , którego przekątna d=8√2 tworzy z bokiem odpowiadającym wysokości walca kat α=60 stopni. Oblicz objętość walca.

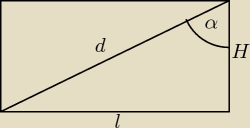
edi: Przypuszczam, że nie miałaś jeszcze funkcji trygonometrycznych, więc wyobraź sobie, że trójkąt utworzony przez przekątną prostokąta jest połową trójkąta równobocznego, rozciętą wzdłuż

	d
wysokości trójkąta równobocznego. Wtedy H =		(wysokość trójkąta równobocznego dzieli
	2

podstawę na dwie równe połowy). Zatem H = 4√2 Następnie z twierdzenia Pitagorasa obliczamy długość l: l² + H² = d² l = √d² − H² I = √128 − 32 l = 4√6

	l		4√6
Wiadomo, że l = 2πr, więc r =		, czyli
	2π		2π

	96		384√2		96√2
Wzór na objętość walca: πr2H = π *		* 4√2 =		=
	4π2		4π		π

edi:

	a√3
Warto pamiętać, że wzór na wysokość trójkąta równobocznego to		, nie trzeba wtedy za
	2

każdym razem korzystać z tw Pitagorasa

proszę o pomoc ważne: uwierz mi ze mialam

Wojtek: 8√2 ile to jest ?