rekurencja nwm: podaj liczbę sposobów wypełnienia planszy o wymiarach 2 × n białymi i czarnymi kostkami o wymiarach 2 × 1 Próbowałem znaleźć wzór rekurencyjny, ale nie mogę go zauważyć

jc: A próbowałeś dla n=1,2,3,4,5 ? Jakie liczby otrzymałeś?

nwm: Dla n = 1 −> 2 n = 2 −> 8 n = 3 −> 24 n = 4 −> 64

jc: Czy na pewno 64? Czy możesz najpierw ułożyć bezbarwne klocki, a potem pokolorować? Na ile sposobów możesz pokolorować n klocków?

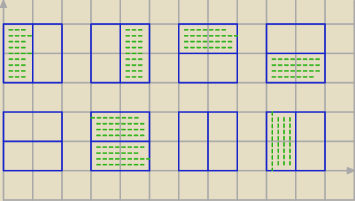
Mila: Czy tak ułożyłeś dla n=2 ?

nwm: tak, tylko to ostatnie to dwa zielone

Mila: Zgadza się, nie pomalowałam do końca. Na kartce mam dwa klocki na zielono. Jutro jeszcze policzę na kratkowanym papierze dla n=3 Ma być od n=0 czy n=1 rekurencja?

Mila: wolfram tak podaje https://www.wolframalpha.com/input/?i=%7B2%2C8%2C24%2C64%2C.....%7D Nie ustalił wzoru, coś jest źle.

Mila: A może przy takim zapisie nie podaje wzoru?

jc: Czy dla 4 nie powinno być 80?

jc: http://oeis.org/search?q=2%2C8%2C24%2C80%2C256&sort=&language=english&go=Search

nwm: rekurencja powinna być od 1

nwm: jc − rzeczywiście − nie policzyłem jednego jeszcze przypadku, przez co wyszło mi 64 a nie 80.

nwm: Bardzo dziękuję za pomoc!

kerajs: Obawiam się, że na kolokwium rozwiązanie przez znalezienie ciągu w OEIS nie będzie punktowane.

jc: Tym bardziej rozwiązanie znalezione na forum.

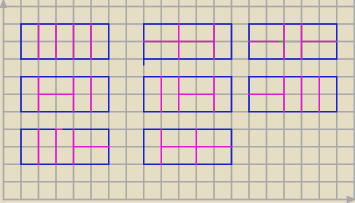
Mila: Plansza 2xn, klocki o wymiarach 2x1 1) n=1 jeden klocek na planszy kolorujemy na biał i czarno na 2¹=2 sposoby a₁=2 2) n=2 dwa klocki na planszy układamy na 2 sposoby ( mamy dwie plansze do pomalowania, na każdej są dwa klocki ) a₂=2²*2=8 3) n=3 trzy klocki na planszy układamy na 3 =(2+1) sposoby a₃=2³*(2+1)=24 4) n=4 cztery klocki na planszy układamy na 5=(2+3) sposoby a₄=2⁴*(2+3)=80 5) n=5 pięć klocków układamy na planszy na 8=(3+5) sposobów a₅=2⁵*8=32*8=256

	an−1		an−2
an=2n*(		+		)
	2n−1		2n−2

Czytajcie i piszcie, gdzie błędne rozumowanie. a_n=2*a_n−1+4*a_n−2 dla n≥3, a₁=2, a₂=8

kerajs: Odpisałbym wcześniej, ale jakiś miły admin zablokował mi konto. Nic to. Rozumowanie nie jest błędne, lecz dla mnie dziwny jest sposób uzyskania rozwiązania. Zwykle wygląda to tak: Układ z n płytkami uzyskuje się dokładając jedną pionową płytkę do układu z n−1 płytkami, lub dwie poziome do układu n−2 płytkowego. Płytkę pionową można dodać na dwa sposoby (białą lub czarną) a dwie poziome na 4 sposoby (dwie białe, tylko górna biała, tylko dolan biała, dwie czarne. Stąd równanie a_n=2a_n−1+4a_n−2 Wzór ogólny uzyska się rozwiązując powyższe z warunkami początkowymi a₁=2, a₂=8