funkcje wiki2020: Podaj zbiór wartości funkcji. Dla jakiego argumentu funkcja przyjmuje swoją wartość najwiekszą lub najmniejszą? a) y = −2(x+1)2 + 5 b) y = 3(x−1)2 −7 c) y = 12(x − π) + 2 d) y = −2√7(x+3)2 − 1 e) y = −4(x + 12)2 − 3 f) y = 0,2(x−2)2 proszę o pomoc

janek191: Np. b) y = 3*( x −1)² − 7 p = 1 q = − 7 a = 3 > 0 więc ZW = < q , + ∞) = < − 7, +∞) Dla x = p = 1 y = y_min

wiki2020: dziękuję bardzo ale mam największy problem z przykładem c,d,e,f nie ogarniam tego

6latek: W jakiej postaci napisane sa te funkcje ? Odpowiedz

wiki2020: kwadratowe ?

6latek: Rownanie kawadratowe mozna zapisac w 3 postaciach 1) ogolna ax²+bx+c=0 2)kanoniczna a(x−x_w)²+y_w=0 3) iloczynowa (x−x₁)(x−x₂)=0 tak samo funkcje mozna zapisac w tych postaciach W ktorej zapisana jest u nas?

wiki2020: kanoniczna chyba

janek191: Postać kanoniczna: y = a*( x − p)² + q W = ( p, q) a> 0 ZW = < q , +∞) dla x = p jest y = y_min dla a < 0 ZW = ( −∞, q> dla x = p jest y = y_max

6latek: dobrze kanoniczna f(x)=a(x−x_w)²+y_w x_w i y_w sa to wspolrzedne wierzcholka a− pokazuje jak beda zwrocone ramiana paraboli Teraz z tej postaci odczytujemy od razu wspolrzedne wierzcholka z tym ze wspolrzedna x_w odczytujemy ze mnienionym znakiem Jesli mamy np a(x−5)²+7 to x_w=5 i y_w=7 Wezmy np twoja e) napisz jakie beda wspolrzedne wierzcholka paraboli czytaj to co napisalem

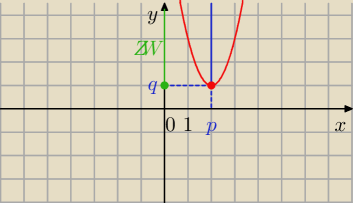
janek191: W = ( p, q ) p = 2 q = 1 a= 2 > 0 Mamy ZW = < q , +∞) = < 1 , +∞) Dla x = p = 2 jest y = q = y_min = 1

wiki2020: 1/1 i −3

6latek: wspolrzena x_w jest nazywana takze p wspolrzedna y_w jest nazywana takze q wobec tego ta postac kaniniczna moze wygladac takze tak y=a(x−p)²+q

wiki2020: przepraszam 1/2 a nie 1/1

6latek: OK .Pomagaj jej

wiki2020: czyli w przykładzie e) bedzie ZW = (−∞; −3> wartość największa −3 dla x = − 12 ?

janek191: Tak

wiki2020: no to chyba coś mi już zaczyna świecić − dziękuję bardzo za pomoc i poświęcony czas