Bryly obrotowe Dream: Wyznacz stosunek objętości kuli do objętości ostroslupa prawidlowego czwrokatnego opisanego na tej kuli, jeśli przekrój ostroslupa zawierajacy dwie jego krawędzie boczne jest trohkatem rownobocznym. Odpowiedź ma wyjść pi(5√7−11)/18

Mila:

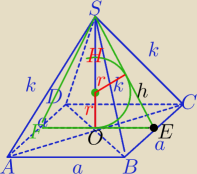
	k√3
1) |AC|=k, H=|OS|=
	2

	k√2
k=a√2⇔a=
	2

2)

	k2
PABCD=
	2

	1		k2		k√3		k3√3
Vo=		*		*		=
	3		2		2		12

3) h−wysokość ściany bocznej:

	a
h2=H2+(		)2⇔
	2

	k√3		k
h2=(		)2+(		)2
	2		2√2

	√7k		√2*√7
h=		=
	2√2		4

4) Promień okręgu wpisanego w ΔEFS

	1
PΔEFS=		a*H=p*r
	2

	a+2k		1		k√2
p=		=		a+k⇔p=		*(1+√7)
	2		2		4

1		k√2		k√3		k√2
	*		*		=		*(1+√7)*r⇔
2		2		2		4

	k√3*(√7−1)
r=
	12

	4
5) Vk=		πr3
	3

	4		k√3*(√7−1)
Vk=		π*(		)3
	3		12

	πk3*√3*(5√7−11)
Vk=
	18*12

Vk		πk3*√3*(5√7−11)		12
	=		*
Vo		18*12		k3*√3

Vk		π*(5√7−11)
	=
Vo		18

□□□□□□□□□□□□

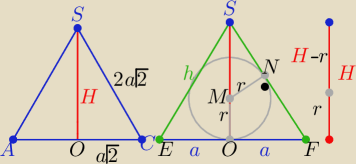Eta: Unikając ułamków wprowadzam oznaczenia : |AB|=2a to |AC=2a√2 z tw. Pitagorasa H=a√6

	1		4		4
Vo=		4a2*a√6 =		√6a3 i Vk=		πr3
	3		3		3

	Vk		π		r
to		=		(		)3
	Vo		√6		a

h²= H²+a² ⇒ h= a√7 Z podobieństwa trójkątów OFS i MNS ( kkk)

r		H−r		r		a√6−r
	=		⇒		=		/*√7
a		h		a		a√7

	r		r		r
√7		= √6−		⇒		(1+√7) =√6
	a		a		a

r		√6
	=		/3
a		√7+1

	r		6√6		6√6(5√7−11)		√6(5√7−11)
(		)3=		=		=
	a		2(5√7+11)		2*54		18

	Vk		5√7−11
to		=		π
	Vo		18

♥♥♥♥♥♥♥♥♥♥♥♥♥♥

Mila: Nie czytasz rozwiązań?