zadania z geometrii kasia0948: W trójkącie równoramiennym między długością k podstawy i długościami h, H dwóch jego nierównych wysokości zachodzi związek k²=h*H. Wyznasz cosinus kąta przy podstawie tego trójkąta. Czy mogłabym prosić o pomoc w rozwiązaniu lub rozwiązanie zadania. Próbowałam używać twierdzeń różnych i ciągle nie wychodzi

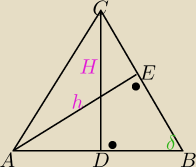
chichi: |AC|=b, |AB|=k, |CD|=H, |AE|=h, k²=hH

1		1		kH
	kH=		bh ⇒ b=
2		2		h

Z ΔADC:

	k
(		)2+H2=b2
	2

k2		k2H2
	+H2=		/ *4h2
4		h2

k²h²+H²4h²−4k²H²=0, dla k²=hH mamy: h³H+H²4h²−4hH³=0 −H(4hH²−4h²H−h³)=0 / : (−H), bo H≠0 4hH²−4h²H−h³=0 Δ_H=16h⁴+16h⁴ ⇒ √Δ_H=4√2h²

	4(√2+1)h2		(√2+1)h
H1=		=		, H2<0
	8h		2

	k2		k		h
cos(δ)=		=		=
	b		2b		2H

	h		1
cos(δ)=		=		=√2−1
	2h(√2+1)2		√2+1

Eta:

	k		H
k2=hH cosα=		i z porównania pól kH=bh ⇒ b= k*
	2b		h

	k2H		H3		h		1		h
to b2=		=		i cosα=		=		(		)
	h		h		2H		2		H

	k2
z tw. Pitagorasa : b2=		+H2
	4

	H3		hH
to		=		+H2 / : H2
	h		4

	H		1	h		h
		=			+1 , podstawiam		= t >0
	h		4	H		H

	1		1
		=		t+1
	t		4

t²+4t−4=0 √Δ=4√2 , t=2(√2−1) >0

	1		h		1
to cosα=		*		=		t
	2		H		2

cosα = √2−1 =============