planimetria sylwia: przekątna trapezu równoramiennego ma długość d i jest prostopadła do jednego z ramion oblicz pole trapezu wiedząc ze kat ostry ma miarę α

Godzio:

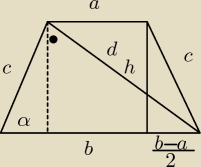
	d
sinα =
	b

	d
b =
	sinα

	c
ctgα =
	d

c = ctgα * d

	b−a   2
cosα =
	c

	d
2cosα * ctgα * d =		− a
	sinα

	d
a =		− 2cosα * ctgα * d
	sinα

	h
sinα =
	c

h = sinα * ctgα * d = cosα*d

	a+b		d   d   − 2cosα * ctgα * d +   sinα   sinα
P =		* h =		* cosα*d =
	2		2

d   cos2α*d   2* − 2 *   sinα   sinα
	* cosα*d =
2

d − cos2d
	* cosαd = (d2 − cos2d2) * tgα = d2 * tgα(1−cos2α) = d2tgα *sin2α
sinα

Sprawdź jeszcze moje wyliczenia czy sie gdzie nie pomyliłem

sylwia:

	1
Dzięki. W odpowiedziach jest ,że powinno wyjść d2 * sinα * cosα [=		d2 sin2α] więc nie
	2

wiem skąd ta rozbieżność

Godzio:

	d
b =
	sinα

	d		cos		d−2cos2d		d(sin2+cos2−2cos2
a =		− 2cosα *		*d =		{ =
	sinα		sin		sin		sin

d(sin2−cos2
sin

	d(sin2−cos2+1)		2sin2d
a + b =		=		= 2sind
	sin		sin

(a+b) * h = 2sinαd*cosαd = sin2α d²

a+b		1
	* h =		sin2αd2 czyli ok w przekształceniu pola się coś pomyliłem, najlepiej
2		2

pokolei a mój błąd znalazłem:

d−cos2αd		cosα		cosα
	* cosαd = d2(1−cos2α) *		= d2 * sin2α *		=
sinα		sinα		sinα

	1
d2sinαcosα =		d2sin2α
	2

sylwia: Wielki dzięki.Pozdrawiam

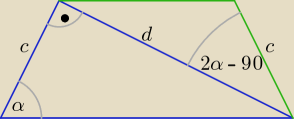Bogdan: c = d*ctgα

	1		1
pole trapezu P =		cd +		cd*sin(2α − 90) = ...
	2		2

sylwia: niby wynik jest dobry ale tok rozumowania nie logiczny dla mnie np:2linijka drugiego posta godzio