z tw sin i cos zadanko: Oblicz cosinusy kątów trójkąta, którego wysokości mają długości 2, 3 i 4.

	11		29		43
odp to −		,		,
	24		36		48

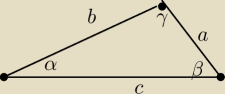
6latek: a=2 b=3 c=4 Twierdzenie cosinusow : Napisz jak brzmi i w ksiazce zobacz wzory .

a7: @6latek to wysokości , anie boki są równe a, b, c

6latek: Przepraszam .Zle przeczytalem

ICSP:

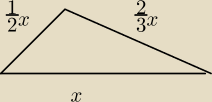
	1		2
wartości		x i		zostały wyznaczone z porównania pola trójkąta.
	2		3

Twierdzenie cosinusów pozwoli na wyliczenie odpowiednich cosinusów.

6latek:

6latek:

	2
Prosze o pokaznie rozwiazania jak zostaly wyliczone wartosci 0,5x i		x.
	3

Znalazlem takie zadanie gdzie dane sa 3 wysokosci i nalezy znalezc podstawowe elementy trojkata tzn boki i kąty wiec stad moglbym policzyc cosinusy kątow . Powiem szczerze masakra .

Eta:

	2*a		3*b		4*c
P=		=		=		⇒2a=3b=4c
	2		2		2

	4
to a=2c, b=		c , c
	3

z tw. cosinusów

	16   4c2+ c2−c2   9		27c2+16c2		43
cosα=		=		=
	4   2*2c* c   3		48c2		48

..................

6latek: Bardzo dziekuje W takim razie mam za madra ksiazke bo autor korzysta tam z ciągu Toporowa .