z tw sin i cos
zadanko: Dany jest trójkąt równoboczny ABC. Punkt D leży na boku BC. Wyznacz tangens kąta DAB, jeśli
stosunek pola trójkąta ADB do pola trójkąta ADC wynosi 1:2.
23 lis 14:58
Eta:
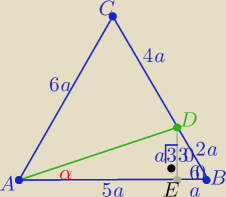
23 lis 15:13
zadanko: Odpowiedzi nie mamy podanej w poleceniu, podałem tylko żeby było wiadomo jaki musi wyjść wynik.
Do odpowiedzi trzeba dojść samemu

23 lis 15:29
Eta:
| | P(ADB) | | 1 | |
Jeżeli |
| = |
| |
| | P(ADC) | | 2 | |
| | |BD| | | 1 | |
to |
| = |
| bo trójkąty mają wspólną wysokość |
| | |DC| | | 2 | |
zatem |BD|= 2a i |DC|=4a więc |AB|=6a
i z trójkąta BDE "ekierkowego" o kątach 60
o,30
o,90
o
|BE|=a, |DE|=a
√3 to |AE|=5a
i otrzymujesz
| | |DE| | | √3 | |
wΔADE : tgα= |
| = |
| |
| | |AE| | | 5 | |
i po ptokach

23 lis 15:48
zadanko: Dobra, dzięki wielkie
23 lis 17:48
Eta:

23 lis 22:19



