pole ab12: Na bokach AB i BC czworokąta wypukłego ABCD zaznaczono odpowiednio punkty E i F tak,że czworokąt BEDF jest równoległobokiem Odcinki AF i EC przecinają się w punkcie G Wykaż że czworokąty BEGF i ADCG mają równe pola

Eta:

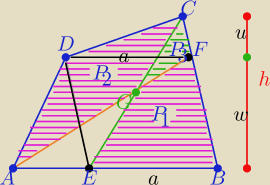
	ah		au		aw		ah
P(ΔEBC)=P1+P3=		i P(ADCF)=P2+P3=		+		=
	2		2		2		2

i mamy tezę P₁+P₃=P₂+P₃ ⇒ P₁=P₂ ========