
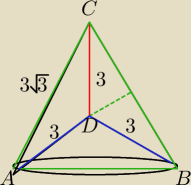
 Po obrocie wokół prostej zawierającej ramię tego trójkąta (zaznaczone na czerwono)
otrzymujemy stożek
o tworzącej 3√3 z wydrążonym stożkiem o tworzącej 3 (długość ramienia obliczamy z
trójkąta ekierki
lub z tw. cosinusów lub z tw. Pitagorasa itp.)
H dużego stożka to H trójkąta równobocznego ABC H=3√3*√3/2=9/2
h małego stożka h=H−CD=4,5−3=1,5
R=3√3/2
V=Vdużego stożka−Vmałego stożka=1/3*π*R2*4,5−1/3*πR2*1,5=πR2=π(3√3/2)2
V=27/4π
Po obrocie wokół prostej zawierającej ramię tego trójkąta (zaznaczone na czerwono)
otrzymujemy stożek
o tworzącej 3√3 z wydrążonym stożkiem o tworzącej 3 (długość ramienia obliczamy z
trójkąta ekierki
lub z tw. cosinusów lub z tw. Pitagorasa itp.)
H dużego stożka to H trójkąta równobocznego ABC H=3√3*√3/2=9/2
h małego stożka h=H−CD=4,5−3=1,5
R=3√3/2
V=Vdużego stożka−Vmałego stożka=1/3*π*R2*4,5−1/3*πR2*1,5=πR2=π(3√3/2)2
V=27/4π
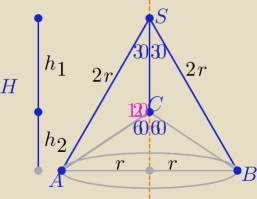
| 3√3 | ||
ΔABS jest równoboczny o boku długości 2r =3√3 ⇒ r= | ||
| 2 |
| 3√3√3 | ||
HΔABS= | = 4,5 | |
| 2 |
| 1 | 1 | |||
V(bryły) = | πr2*H − | πr2*h1 | ||
| 3 | 3 |
| 1 | ||
V(bryły)= | πr2*3 | |
| 3 |
| 27 | ||
V=πr2= ..= | π | |
| 4 |