Wyjaśnienie
zadanko: Przekątne czworokąta wypukłego podzieliły go na cztery trójkąty. Promienie okręgów opisanych na
tych trójkątach są równe 5. Oblicz długości boków czworokąta.
Odp: Czworokąt jest rombem o boku 10
Potrzebuję jedynie wyjaśnienia skąd wiemy, że czworokąt jest rombem

22 lis 18:54
Eta:
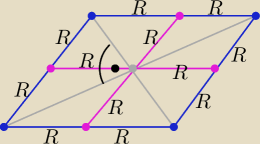
22 lis 19:10
kerajs:
@Eta
Ten rysunek niczego nie wyjaśnia. On ilustruje implikację przeciwną: skoro czworokąt jest
rombem to okręgi opisane na trójkątach (uzyskanych z podziału rombu przez przekątne) mają
takie same promienie.
22 lis 19:19
a7:
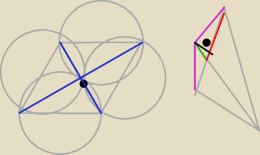
Wiemy, że przekątne rombu przecinają się na połowy pod kątem prostym tworząc cztery przystające
trójkąty
prostokątne. Połowa przeciwprostokątnej to promień okręgu opisanego na takim trójkącie, a więc
cały bok rombu będzie miał 10
Można po prostu wpaść na to (zauważyć), że romb spełni nasze warunki zadania, i inny czworokąt
nie,
jako że promień okręgu opisanego na trójkącie
R=abc/4P a nasze trójkąty mają "parami równe boki" i tylko gdy wszystkie będą przystające (jak
w rombie) to promień będzie równy sobie
gdyż :
R
1=a
1b
1c
1/4P
1 P
1=1/2*c
1*h
1 h1=h2 R
1=a
1b
1/(2h
1)
R
2=a
1b
2c
2/4P
2 P
2=1/2c
2*h
1 a1=a2 R
2=a
1b
2/(2h
1)
czyli b
1 musi być równe b
2(oraz równe b
3 i b
4, b
2=b
3 i b
4=b
1) oraz c
1=c
2=c
3=c
4 ,
skoro R
1=R
2=R
3=R
4
c.n.w.
22 lis 19:26
ABC:
o widzę że Leon zawodowiec coś wyczyścił znowu ... faktycznie wzorowanie się na Himmilsbachu do
niczego dobrego nie prowadzi , pamiętam jeszcze z młodych lat siędzę sobie w empiku i nagle
wpada gość i zasuwa tekst do obecnej tam kobiety : "Ty k...o dawaj pięćset złotych "

22 lis 20:01
kerajs: Szkoda, że przy okazji usunięto także fragment o brakach ''dowodu'' a7.
@Eta
Wykasowywanie niewygodnych postów jest passé. Skoro ja, dziecina, słyszałem o kindersztubie, to
Ty pewnie ją świetnie znasz i wiesz jak powinnaś się zachować.
PS
Gdzie leżą wierzchołki trójkątów? Jeden to część wspólna czterech okręgów, a pozostałe .... .
Aby trzy punkty leżały na prostej .....
23 lis 07:28


 Wiemy, że przekątne rombu przecinają się na połowy pod kątem prostym tworząc cztery przystające
trójkąty
prostokątne. Połowa przeciwprostokątnej to promień okręgu opisanego na takim trójkącie, a więc
cały bok rombu będzie miał 10
Można po prostu wpaść na to (zauważyć), że romb spełni nasze warunki zadania, i inny czworokąt
nie,
jako że promień okręgu opisanego na trójkącie
R=abc/4P a nasze trójkąty mają "parami równe boki" i tylko gdy wszystkie będą przystające (jak
w rombie) to promień będzie równy sobie
gdyż :
R1=a1b1c1/4P1 P1=1/2*c1*h1 h1=h2 R1=a1b1/(2h1)
R2=a1b2c2/4P2 P2=1/2c2*h1 a1=a2 R2=a1b2/(2h1)
czyli b1 musi być równe b2(oraz równe b3 i b4, b2=b3 i b4=b1) oraz c1=c2=c3=c4 ,
skoro R1=R2=R3=R4
c.n.w.
Wiemy, że przekątne rombu przecinają się na połowy pod kątem prostym tworząc cztery przystające
trójkąty
prostokątne. Połowa przeciwprostokątnej to promień okręgu opisanego na takim trójkącie, a więc
cały bok rombu będzie miał 10
Można po prostu wpaść na to (zauważyć), że romb spełni nasze warunki zadania, i inny czworokąt
nie,
jako że promień okręgu opisanego na trójkącie
R=abc/4P a nasze trójkąty mają "parami równe boki" i tylko gdy wszystkie będą przystające (jak
w rombie) to promień będzie równy sobie
gdyż :
R1=a1b1c1/4P1 P1=1/2*c1*h1 h1=h2 R1=a1b1/(2h1)
R2=a1b2c2/4P2 P2=1/2c2*h1 a1=a2 R2=a1b2/(2h1)
czyli b1 musi być równe b2(oraz równe b3 i b4, b2=b3 i b4=b1) oraz c1=c2=c3=c4 ,
skoro R1=R2=R3=R4
c.n.w.
