z tw sin i cos zadanko: W trójkącie ABC dane są długości boków AB=12, AC=8, BC=10. Dwusieczna kąta ACB przecina bok AB w punkcie D. Oblicz długość odcina CD.

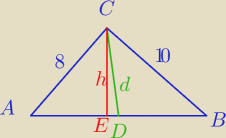
janek191: I AD I = x I DB I = 12 − x = y Mamy

x		8
	=
12 −x		10

	1
x = 5
	3

	2
y = 6
	3

I ED I = z Mamy

	20
102 = (		+ z)2 +h2
	3

	16
82 = (		− z)2 + h2
	3

Otrzymujemy

	5
z =
	6

więc h² = 43,75 oraz

	2
d = 6
	3

==============

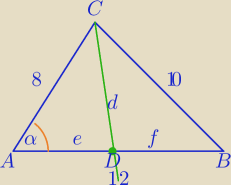
Mila: II sposób 1) Z tw. o dwusiecznej kąta w Δ

e		8
	=		i e+f=12
f		10

	16		20
e=		i f=
	3		3

2) W ΔABC: tw. cosinusów 10²=8²+12²−2*8*12 *cosα

	9
cosα=
	16

3) W ΔADC: z tw. cosinusów

	16		16		9
d2=(		)2+82−2*		*8 *
	3		3		16

	400
d2=
	9

	20
d=
	3

======

Eta: 3 sposób z porównania pól P₁=4dsinα , P₂=5dsinα to P=9dsinα i P=40sin(2α)= 80sinαcosα ( bo sin(2α)=2sinαcosα 9d=80cosα

	64+100−144		1
cos2α=		=		−− trójkąt ostrokątny
	2*8*10		8

2cos²α−1=cos(2α) ⇒ cosα= 3/4>0 9d=60

	20
d=
	3

=========

zadanko: Dziękuję