z tw. sin i cos zadanko: W czworokącie ABCD, gdzie |AB| = |BC| = 27, |CD| = 26, |DA|=24. Dwusieczna kąta BAD zawarta jest w prostej AC. Oblicz długość przekątnej AC.

Eta: |AC|=30

zadanko: Wynik znam, potrzebuję sposoby rozwiązania

Eta:

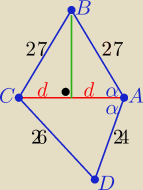
	d
ΔABC równoramienny i d=27*cosα ⇒ cosα=
	27

W ΔADC z tw. cosinusów

	4d2+242−262
cosα=
	2*2d*24

d		d2−25
	=
27		24d

3d²=25*27 d=15 |AC|=2d=30 ==========

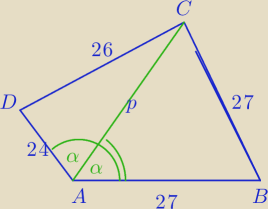
Mila: Z tw. cosinusów w ΔBAC: 27²=p²+27²−2*27*p*cosα⇔0=p²−54p*cosα, p>0

	p
p=54 cosα⇔cosα=
	54

W ΔDAC:

	p
262=p2+242−2p*24*
	54

p=30 lub p=−30∉D