Rozwiązywanie nierówności zmartwionyuczeń: Jest jakiś sposób, żeby rozwiązać tę nierówność szybciej niż rozpatrywanie wszystkich przypadków? ^(m−2)(m+1)_2m+1 ≤ 0 Rozpatrywanie wszystkich przypadków w sensie:

⎧	(m−2)(m+1) ≥ 0
⎩	2m+1 < 0

i

⎧	(m−2)(m+1) ≤ 0
⎩	2m+1 > 0

Rozwiązując tym sposobem trochę to schodzi + jest sporo rachunków, więc można się pomylić, a mam przeczucie, że jest znacznie łatwiejszy sposób, którego nie dostrzegam.

ICSP:

(m−2)(m+1)		1
	≤ 0 i m ≠ −
2m+1		2

(2m+1)(m−2)(m+1) ≤ 0

	1
m ∊ (− ∞ ; −1] ∪ (		;2]
	2

6latek:

a
	≤0⇔a*b≤0 i b≠0
b

Twoim sposbem mozna to rozwiazc w pamieci pomagajac sobie lekko na kartce

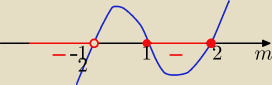
Eta: (m−2)(m+1)(2m+1)≤0

zmartwionyuczeń: Dlaczego można pomnożyć przez (2m+1)? Przecież nie wiemy jaki znak będzie miała ta liczba

zmartwionyuczeń: Aaaa, pomnożyliście przed kwadrat. Jestem upośledzony. XD Dziękuję!

Eta:

6latek: Nie pisz tak o sobie bo w to naprawde uwierzysz Ja np nie mialem na mysli kwadratu mianownika (chociaz TY mozesz miec) Po prostu znak ilorazu jest taki sam jak znak iloczynu Nalezy jednak uwazac przy zwrocie nierownosci ≤ lub ≥ Tutaj nalezy dodac warunek mianownik≠0 i bedzie wtedy to rownowazne