pole trójkąta DAniel: W trójkącie ABC o danym polu S na bokach BC, CA, AB obrano odpowiednio punkty D, E, F w taki

	|BD|		|CE|		|AF|
sposób, że		=		=		=k, k>0. Oblicz pole trójkąta DEF
	|DC|		|EA|		|FB|

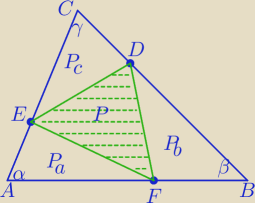Mila: P_DEF=S−(P_a+P_b+P_c}

	|AF|
1)		=k
	|FB|

|AF|		k*|FB|		k
	=		=		⇔
|AB|		k*|FB|+|FB|		k+1

	k
|AF|=		*|AB|
	k+1

=========== 2)

CE|
	=k
|AE|

|AE|		|AE|		1
	=		=		⇔
|AC|		|AE|+k*|AE|		k+1

	1
|AE|=		*|AC|
	k+1

===============

CE		|k*|AE|		k
	=		=
|AC|		|AE|+k*|AE|		k+1

	k
|CE|=		*|AC|
	k+1

=============== 3)

|BD|
	=k
|DC|

4)

|BD|		k*|CD|		k
	=		=
|BC|		k*|CD|+|CD|		k+1

	k
|BD|=		*|BC|
	k+1

	1
|CD|=		*|BC|
	k+1

5) Korzystamy ze wzoru na pole z sinusem odpowiedniego kąta

	1
Pa=		|AF|*|AE|*sinα⇔
	2

	1		k		1
Pa=		*		*|AB|*		*|AC|*sinα⇔
	2		k+1		k+1

	k
Pa=		*S
	(k+1)2

============

	1		1		1		k
Pb=		*|FB|*|BD|*sinβ=		*		|AB|*		*|BC|*sinβ
	2		2		k+1		k+1

	k
Pb=		*S
	(k+1)2

=============

	1		1		1		k
Pc=		*|CD|*|CE|=		*		*|BC|*		*|AC|*sinγ
	2		2		k+1		k+1

	k
Pc=		*S
	(k+1)2

============= 5)

	3k
P=S−		*S
	(k+1)2

	3k
P=S*(1−		)
	(k+1)2

============= Może sprawdź, czy wyrażenie w nawiasie jest dodatnie dla każdego k>0.

DAniel: dzięki

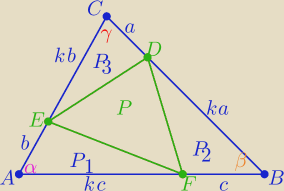Eta: |AB|=c(k+1) , |AC|=b(k+1) , |BC|=a(k+1) 2S= |AB|*|AC|*sinα=bc(k+1)²*sinα i 2 P₁=bck*sinα 2S= |BC|*|AB|*sinβ=ac(k+1)²*sinβ i 2P₂=ack*sinβ 2S= |BC|*|AC|*sinγ =ab(k+1)²*sinγ i 2P₃=abk*sinγ to

	P1		P2		P3		k		3k
		=		=		=		to P1+P2+P3=		S
	S		S		S		k+1)2		(k+1)2

zatem P=S−(P₁+P₂+P₃)

	3k
P= S(1−		)
	(k+1)2

================