porządki salamandra: Dana jest relacja porządkująca na zbiorze R² punktów na płaszczyźnie {(x₁ , y₁ ), (x₂ , y₂ ) : x₁ ≤ x₂ ∧ y₁ ≤ y₂ }. Wyznacz elementy minimalne i maksymalne zbioru. Czy zbiór posiada elementy najmniejsze i największe? c) {(x, y) : x²+y²≤1} To będzie koło o promieniu 1, ale nie wiem jak na podstawie punktów określić, czy posiada elementy największe, czy najmniejsze − patrzymy na x, czy na y?

Maciess: Przede wszystkim czy umiesz sobie zwizualizować tak zadany porządek graficznie? Druga sprawa definicja elementów min/max i największy najmniejszy. Znasz różnice?

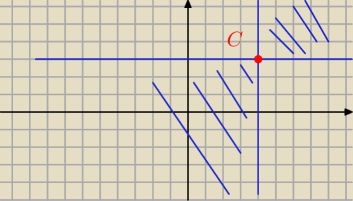
Maciess: Czerwony punkt (C) to jakis ustalony element R². W niebieskim obszarze znajdują się punkty porównywalne z C.

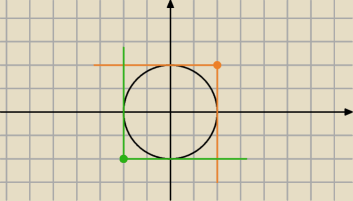
Maciess: Zielony i pomarańczowy punkt, to jacys pretendenci do bycia elementem (odpowiednio) najmniejszym i największym). Jak widac nie nalezą do zbioru. Pobaw się podobnie i poszukaj elementów minimalnych/maksymalnych

salamandra: Znam różnice pomiędzy maksymalnym, minimalnym. największym, natomiast patrząc na to koło nie wiem jak określić, który jest najmniejszy i największy − nie wiem czy ważniejsza jest tu współrzędna x czy y. Intuicyjnie obstawiałbym punkt (0,1) jako największy, ale pewnie źle myślę

Maciess: Mhm... Czyli dalej nie rozumiesz. No dobra typujesz (0,1). A ja mowie, ze jest nieporównywalny z punktem (1,0). Czyli nie moze byc najwiekszy.

salamandra: Dlaczego jest nieporównywalny? Przepraszam, ale tych przykładów z punktami na płaszczyźnie nie rozumiem

ABC: czy zachodzi (0,1)R(1,0) ? a może zachodzi (1,0)R(0,1) ?

salamandra: Ahaa, zapomniałem o treści zadania −−− no nie zachodzi, co nie zmienia faktu, że nadal nie wiem jak ustalić te elementy maksymalne i minimalne w tym przypadku

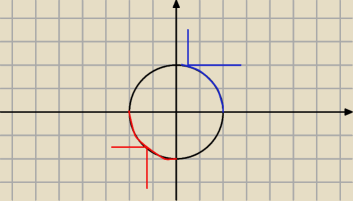
Maciess: Dla dowolnego punktu ze zbioru zaznaczonego na czerwono, nie istnieje element mniejszy. Dla dowolnego punktu ze zbioru zaznaczonego na niebiesko, nie istnieje element większy.

salamandra: czyli na tych liniach co narysowałeś musiałby istnieć ten punkt, aby był porównywalny z tym punktem, który zaznaczyłeś?

Maciess: Patrz jeszcze raz post wczoraj z 22:53. Tam jest zaznaczony obszar gdzie leża punkty porównywalne z nim. "na lewo i w dół" sa punkty mniejsze od niego, "na prawo i do góry" są większe. Na rysunku wyzej zaznaczylem tylko fakt, ze w tym zbiorze czerwonym nie masz juz mniejszych elementów. Bo w obszarze na "na lewo i na dół" nie ma juz punktów z tego okręgu.

salamandra: Czyli żeby dany punkt był większy od innego, to zarówno współrzędna x jak i y musi być większa? Czy zależy to tylko i wyłącznie od warunku w zadaniu i w moim zadaniu z racji na x₁ ≤ x₂ i y₁≤y₂ jest akurat tak?

Maciess: Do pierwszego pytania. Tak (równość też wystarczy), to jest dosłowne odczytanie warunku twojej relacji. Drugiego pytania nie rozumiem. Zadanie rozwiązałem ci praktycznie całe. Kwestia jest taka, że ty nie rozumiesz jak ta relacja działa. Spróbuj sie pobawic w rysowanie na płaszczyźnie i sobie jakoś to przyswoić. Jak nie będzie szło, to wybierz się do ćwiczeniowca na konsultacje. Może na żywo będzie ci w stanie to lepiej wytłumaczyc.

salamandra: Znaczy już rozumiem, jakbyś jeszcze mógł mi pokazać, jak by to wyglądało, jeśli by był warunek x₁≤x₂ ∧ y₁ ≥y₂ to byłbym wdzięczny. Czy wtedy elementem maksymalnym byłby (1,0) i (0,−1)?

Maciess: Narysuj sobie punkt na płaszczyźnie i zaznacz obszar gdzie są punkty większe od twojego punktu. Wszystko będzie jasne. To które wymieniles to tylko 2 maksymalne. Jest ich więcej

xxx: δγ≥≥≥≥≥≥≥≥≥≥≥≥≥δγ≥≥≥≥≥≥≥≥≥≥≥≥≥δγ≥≥≥≥≥≥≥≥≥≥≥≥≥δγ≥≥≥≥≥≥≥≥≥≥≥≥≥δγ≥≥≥≥≥≥≥≥≥≥≥≥≥δ γ≥≥≥≥≥≥≥≥≥≥≥≥≥δγ≥≥≥≥≥≥≥≥≥≥≥≥≥δγ≥≥≥≥≥≥≥≥≥≥≥≥≥δγ≥≥≥≥≥≥≥≥≥≥≥≥≥δγ≥≥≥≥≥≥≥≥≥≥≥≥≥δγ≥≥≥≥≥≥≥≥≥≥≥≥ALE Z WAS CEPY≥δγ≥≥≥≥≥≥≥≥≥≥≥≥≥δγ≥≥≥≥≥≥≥≥≥≥≥≥≥δγ≥≥≥≥≥≥≥≥≥≥≥≥≥δγ≥≥≥≥≥≥≥≥≥≥≥≥≥

salamandra: Hm, a to nie będą w tym momencie punkty w II ćwiartki i z IV?

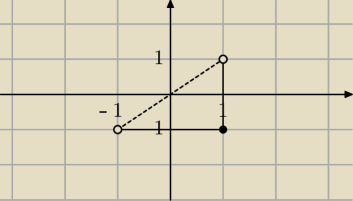
salamandra: a) {(x, y) : −1 ≤ x ≤ 1 ∧ −1 ≤ y < x} W tym przykładzie wyszło mi coś takiego: czy to oznacza, że relacja nie posiada elementu minimalnego, maksymalnego, najmniejszego i największego, a sytuacja zmieniłaby się dopiero, gdy (−1,−1) i (1,1) należałyby do relacji?