wykazywanie Gmx: W okrąg wpisano trójkąt równoboczny ABC a następnie na krótszym łuku AB wybrano punkt D Prosta CD przecina bok AB w puncie E

	1		1		1
Wykaż że zachodzi równość		+		=
	AD		BD		ED

chichi: Jaki to niby krótszy łuk? Łuki: AB, BC i AC są równej długości!

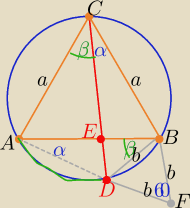
Eta: 1/ rysunek 2/ z tw. Talesa w ΔABF

b		b+AD
	=		i b=|BD|
ED		AD

	b		b
		=		+1 / : |BD|
	ED		AD

i mamy tezę

	1		1		1
		=		+
	ED		AD		BD

=============

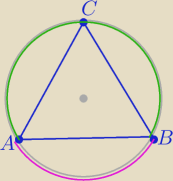
Eta: @chichi

6latek: Wydaje mi sie ze rowne kąty srodkowe sa oparte na rownych lukach . Wedlug mnie powinno byc A nastepnie na łuku AB itd

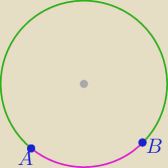
Eta: Dwa punkty na okręgu wyznaczają dwa łuki krótszy i dłuższy Koniec rozważań ! W matematyce nie używamy słowa "wydaje mi się" Jest "tak" , albo "nie"

Jerzy: 14:57 , masz rację, ale to nie ma nic wspólnego z tym zadaniem

6latek: Dobrze Eta Wiec uwazasz ze luk AB w tym zadaniu jest krotszy od luku BC i CA? Dlaczego? Wedlug mnie sa rowne .

chichi: @Eta już rozumiem, myślałem po prostu, że punkt C w tym wszystkim uczestniczy, a tutaj chodzi tylko o podział okręgu na łuki wyznaczone przez punkty A i B

chichi: Według mnie to za mało doprecyzowane stąd ta nieścisłość, ale mogę się mylić.

6latek: OK. Teraz rozumiem .

chichi: @Eta15:25 istnieje też taki podział przez dwa punkty, który dzieli okrąg na łuki tej samej długości, nie koniecznie krótszy i dłuższy

Eta: A to już nie ma związku z tym zadaniem

6latek: