znajdz rownania bokow misia: hej, proszę o pomoc w zadaniu w trójkącie ABC dane jest: wierzchołek A=(1;0), równanie x+3y−13=0 boku BC i wektor wysokości CD=[2;−2], znajdz rownanie pozostalych boków, dziękuję z góry za pomoc

6latek: Moze ktos zrobic rysunek do tego zadania zwlaszcza chodzi o ten wektor CD Podziekowal

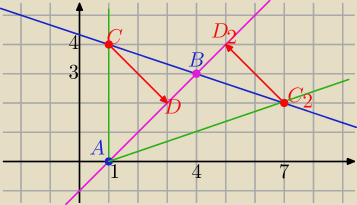
Eta: → CD=[2,−2] AB: x−y−1=0 AC: x=1 BC: x+3y−13=0 warunek zadania spełnia C(1,4) → Punkt C₂(7,2) nie spełnia warunku bo CD= [−2,2]

6latek: Bardzo dziekuje.

Eta: AB: 2(x−1)−2(y−0)=0 AB: x−y−1=0 |CD|=2√2 Odległość punktu C od prostej AB jest równa d=2√2 C∊pr. BC BC: x+3y−13=0 to C(13−3y,y) oraz AB : x−y−1=0

	|13−3y−y−1|
i mamy:		=2√2
	√2

|12−4y|=4 /:4 ⇒ |y−3|=1 ⇒ y=4 v y=2 to x=13−12=1 v x=13−6=7 C(1,4) v C(7,2) −−− nie spełnia warunku zadania A(1,0) , C(1,4) to AC: x=1 Wyżej podałam rys. i odpowiedzi

Misia: Bardzo dziękuję! Nie wiedziałam w ogóle jak się za to zabrać:(

Eta: