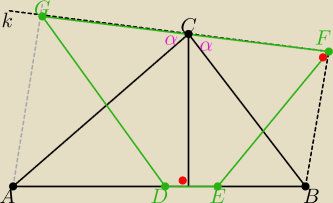
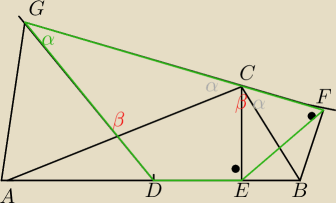
dowód tobiaszek: Dany jest trójkąt ABC, którego boki spełniają warunek |AB|>|AC|>|BC|. Przez wierzchołek C trójkąta ABC przeprowadzono prostą k, która tworzy z bokami AC i BC takie same kąty. Na prostych AB i k wybrano odpowiednio po dwa punkty D i E oraz F i G takie, że |AD|=|BD|, CE ⊥ AB, BF ⊥ k oraz DG ∥ BC. Uzasadnij, że na czworokącie DEFG można opisać okrąg oraz, że AG ⊥ k.

a7: ale gdzie jest punkt E, CE⊥AB?

a7:

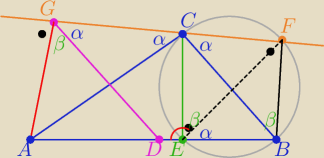Eta: α+β=90^o ( dlaczego ? |∡DGC|=α ( dlaczego? |∡DEF|=90^o+β α+90^o+β= .... i mamy tezę Komentarze dopisz samodzielnie