Boki trójkąta mają 2,3 i 4 cm jaką długość ma wysokość trójkąta opuszczona na na
Zairox: Boki trójkąta mają 2,3 i 4 cm jaką długość ma wysokość trójkąta opuszczona na najdłuższy bok?
19 lis 12:47
ICSP: 1. Policz pole trójkąta wykorzystując wzór Herona
2. Oblicz szukaną wysokość za innego wzoru na pole.
19 lis 12:55
mr t:
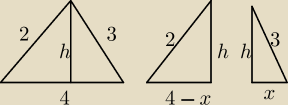
ewentualnie rozbijasz na dwa trojkaty prostokatne, ukladasz uklad 2 rownan z dwiema
niewiadomymi
19 lis 13:04
a7: można też skorzystać z tw, cosinusów
| | 13 | |
42−22+32−2*2*3cosα ⇒ cosα= |
| |
| | 12*16 | |
P=1/2*2*3cosα=13/64
| | 5 | |
P=1/2*4*h=13/64 h=1 |
| (cm) |
| | 8 | |
19 lis 13:11
chichi: @a7 skąd ten wzór P=1/2*2*3cosα=13/64?
19 lis 13:16
a7: ojej pomyliło mi się z sinusem.....
miało być 1/2*2*3*sinα, ale widzę, że tu już więcej roboty, nie ma sensu,
dzięki za wychwycenie... i sorki za zaśmiecenie wątku
19 lis 13:19
19 lis 13:20
chichi: @
a7 ja wiem czy dużo? z jedynki tryg. wyliczyć szybko sinusa i w prawdzie mamy gotowy
wynik

19 lis 13:21
6latek: No fajnie

Ale czy sprawdzono na poczatku czy taki trojkat istnieje?
Widzialem juz wiele takich podchwytliwych zadan
19 lis 13:31
a7: dobra poprawiam
4
2=2
2+3
2−2*2*3cosα cosα=−1/4
sinα=
√1−1/16=
√154
P=1/2*2*3*sinα=1/2*2*3*
√15/4=3
√15/4 1/2*4*h=3
√15/4 h=3
√15/8

ech
19 lis 13:33
Eta:
Połowa obwodu

=9/2
| | 1 | |
PΔ= |
| *4*h =2h i P=√p(p−a)(p−b)(p−c) |
| | 2 | |
| | 3 | |
2h=√(9/2)*(5/2)(3/2)*(1/2) ⇒2h= |
| √15 |
| | 4 | |
==========
19 lis 13:34
Eta:
Trójkąt o bokach: 2,3,5 −−− nie istnieje
Trójkąt o bokach: 2,3,4 −− istnieje i jest rozwartokątny bo 22+32<42
19 lis 13:36
Eta:
Sorry , tam zamiast "jęzora" miało być p=9/2
19 lis 13:39
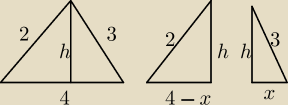 ewentualnie rozbijasz na dwa trojkaty prostokatne, ukladasz uklad 2 rownan z dwiema
niewiadomymi
ewentualnie rozbijasz na dwa trojkaty prostokatne, ukladasz uklad 2 rownan z dwiema
niewiadomymi

 Ale czy sprawdzono na poczatku czy taki trojkat istnieje?
Widzialem juz wiele takich podchwytliwych zadan
Ale czy sprawdzono na poczatku czy taki trojkat istnieje?
Widzialem juz wiele takich podchwytliwych zadan
 ech
ech
 =9/2
=9/2