Wartość bezwzględna spójnik
Dawid: Witam mam takie zadanie i wszystko mam dobrze oprócz spójnika kiedy suma, a kiedy część wspólna
Postanowiłem umieścić spójnik ⋀, a w odpowiedzi jest suma przedziałów ⋁, od czego to zależy.
Dziękuję za odp
Zadanie:
x2−5*|x|≤−6
17 lis 16:35
chichi: A widzisz tam ten moduł?
17 lis 16:52
moneta:
x
2=|x|
2
|x|
2−5|x|+6≤0
(|x|−2)(|x|−3)≤0
|x| ∊<2,3>
|x|≤3 ∧ |x|≥2
x∊<−3,3> ⋀ x∊( −
∞, −2>U <2,
∞)
część wspólna jest odpowiedzią :
x∊<−3,−2> U< 2,3>
===================
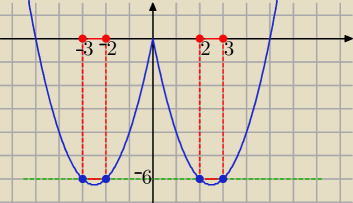
Na rys. sposób graficzny
x
2−5|x|≤ −6
17 lis 16:54
Dawid: Ja zrobiłem to, że rozłożyłem to na dwa przypadki, czyli 1' x≥0 2' x<0
i wyszły mi dwa przedziały z 1' x∊<2;3> z 2' x∊<−3;−2>
Czy tak jak to zrobiłem, czy tak w ogóle można?
17 lis 17:47
chichi: Oczywiście, że można, tylko sposób @
moneta jest dużo lepszy, szybszy, aczkolwiek twój też
jest poprawny, u Ciebie odp. jest część wspólna obu przypadków

17 lis 17:55
chichi: Pfff.... suma obu przypadków oczywiście*

17 lis 17:58
Eta:

17 lis 18:09
Dawid: Właśnie sposobu @moneta nie rozumiem jeszcze nie ten poziom, ale jak przy tym moim sposobie
określić spójnik?
17 lis 18:23
Dawid: Ok już ogarnąłem, ogólnie mam na spójnik taki sposób obracam go zgodnie ze wskazówkami zegara
o 90st. Ale teraz już wiem, to sprawdza się tylko, kiedy występuje nieciągłość w przedziałach.
Teraz już wiem że kiedy występuje ciągłość w przedziałach to muszę odwrócić w lewo.
17 lis 18:51
 x2=|x|2
|x|2−5|x|+6≤0
(|x|−2)(|x|−3)≤0
|x| ∊<2,3>
|x|≤3 ∧ |x|≥2
x∊<−3,3> ⋀ x∊( −∞, −2>U <2,∞)
część wspólna jest odpowiedzią :
x∊<−3,−2> U< 2,3>
===================
Na rys. sposób graficzny
x2−5|x|≤ −6
x2=|x|2
|x|2−5|x|+6≤0
(|x|−2)(|x|−3)≤0
|x| ∊<2,3>
|x|≤3 ∧ |x|≥2
x∊<−3,3> ⋀ x∊( −∞, −2>U <2,∞)
część wspólna jest odpowiedzią :
x∊<−3,−2> U< 2,3>
===================
Na rys. sposób graficzny
x2−5|x|≤ −6


