Geometria analityczna tomek123098: Czesć, mam podane współrzędne wierzchołków A(−1, 2, 5) i B(1, 6, −3) oraz znam punkt przecięcia środkowych S(2, 4, 0). Mam wyznaczyć współrzędne wierzchołka C. Póki co wyznaczyłem środek boku AB − punkt P o współrzędnych (3, 3, 3/2). Nie wiem jak to teraz wszystko zebrać do kupy i wykorzystać.

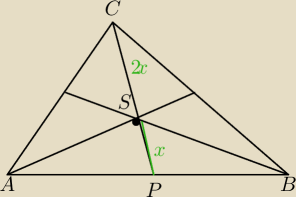
a7: nie znam się na trójwymiarowej geometrii analitycznej ale chyba jeśli poprowadzimy ze środka AB prostą do wierzchołka C to punkt C będzie równy trzem odległościom PS gdyż środkowe dzielą się w stosunku 2:1 czyli liczymy długość PS PC=3*|PS| (CS=2*|CS|) i podstawiamy i chyba powinno wyjść

6latek:

	xp+xc
xs=
	2

	yp+yc
ys=
	2

	zp+zc
zs=
	2

wyliczasz x_c y_c i z_c

6latek: Dzien dobry a₇

a7: @6latek ale S to nie środek odcinka CP tylko punkt przecięcia środkowych

tomek123098: Środkowe zawsze dzielą się w stosunku 2:1?

a7: Dzień dobry

a7: tak

a7: jest tw o środkowych

6latek: Przepraszam masz racje .To nie srodek odcinka

a7: a gdyby podzielić na trzy?

a7: a czy P nie ma wpsółrzędnych (0,4,1) ?

a7: S i P mają te samą współrzędną y to i C będzie miało tę samą wspólrzędną y=4 (?)

jc:

	1
S=		(A+B+C)
	3

C=3S − A − B

a7: i pozamiatane

tomek123098: Dzieki za pomoc

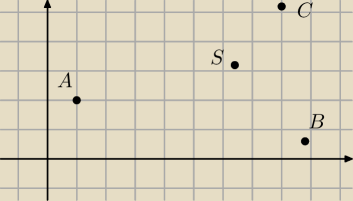
6latek: Srodek ciezxkosci trojkata to punkt przciecia sie srodkowych Wspolrzedne tego punktu mozna wyprowadzic ze wzorow na podzial odcinka w odpowiednin stosunku To mozna sobie znaleac w odpowiedniej literaturze (jesli ktos chce ) Tutaj A=(x₁,y₁,z₁) B=(x₂,y₂,z₂) C=(x₃,y₃,z₃) S=(x₀,y₀ z₀ woiec

	x1+x2+x3
x0=		to x3=
	3

	y1+y2+y3
y0=		to y3=
	3

	z1+z2+z3
z0=		to z3= Trzeba tylko podstawic odpowiednie wartosci
	3

Przy wyprowadzaniu wzorow na srodek ciezkosci trojkata korzystamy z twierdzenia ze srodek siezkosci trojkata jet punktem przecia jego trzech srodkowych i dzieli kazda z nich w stosunku 2: 1

Mila: 1) A=(−1, 2, 5) , B=(1, 6, −3), C=(x_c,y_c,z_c) 2)

	−1+1+xc		2+6+yc		5−3+zc
S=(2,4,0)=(		,		,		)
	3		3		3

x_c=6, y_c=4,z_c=−2 C=(6,4,−2) ===========