Dowód w oparciu o definicję granicy ciągów Shizzer: Przerabiam sobie granice ciągów nieskończonych z Krysickiego i Włodarskiego. Jest sobie takie zadanie: Wykazać, że jeżeli dla ciągu {u_n} istnieje granica:

	un + 1
limn→∞|		| = q < 1,
	un

to lim_n→∞ u_n = 0. Jest podane rozwiązanie i brzmi ono tak: "Weźmy pod uwagę ciąg bezwzględnych wartości wyrazów danego ciągu: {|u_n|}. Ciąg ten od pewnego miejsca musi być malejący, ponieważ na podstawie definicji granicy dla każdego ε istnieje takie N, że

	un + 1
|		| ≤ q + ε dla n ≥ N
	un

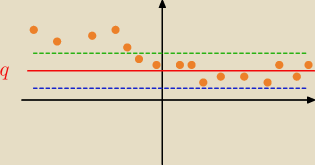
(...)" Nie rozumiem dlaczego ten ciąg musi być malejący. Naszkicowałem rysunek, który odzwierciedla definicję granicy ciągu nieskończonego. Zielona przerywana linia to q + ε, a niebieska q − ε.

	un + 1
Wyrazu ciągu |		| mogą zmierzyć do q POD prostą q LUB NAD nią. Wtedy
	un

ciąg staje się niemonotoniczny. Ktoś mógłby mi wytłumaczyć dlaczego ten ciąg {u_n} jest malejący? Bo w ogóle tego nie rozumiem

Shizzer: Już rozumiem skąd ciąg u_n jest malejący. To wynika właśnie z definicji ciągu nieskończonego. Gdyby ktoś miał problem ze zrozumieniem dlaczego tak jest to wyjaśnię jak ja do tego doszedłem:

	un + 1
||		| − q| < ε (dla każdego ε > 0) dla każdego n ≥ N
	un

	un + 1
|		| < q + ε
	un

Skoro q < 1 ∧ ε > 0, a rozważamy powyższe równanie dla każdego ε to, możemy wziąć tak mały ε, że q + ε = 1. Wtedy:

	un + 1
|		| < 1 ⇒ un + 1 < un, zatem ciąg un jest malejący.
	un

Przykład: u₁ = 8 <− n = 1 u₂ = 6 <− u_{n + 1} < u_n, teraz n = 2 u₃ = 5 <− u_{n + 1} < u_n, teraz n = 3 itd.

jc: Załóż dla uproszczenia, że u_n>0. Jeśli 0 < q < 1, to weźmy d pomiędzy q < d < 1. Ponieważ U_n+1/u_n → q, więc dla n większych od pewnego m, u_n+1/u_n < d u_n < d^n−m u_m →0 przy n→∞

Shizzer: Jest dalsza część rozwiązania zadania, której już kompletnie nie pojmuję: "Ciąg {|u_n|} jako malejący (to już sobie udowodniłem) i ograniczony liczbą 0, musi mieć granicę nieujemną, skończoną. Twierdzimy, że granicą tą musi być 0, gdyż jeśli |{u_n}|→g, to: |u_{n + 1}|→g (...)" Skąd się to wzięło? Nie rozumiem totalnie

jc: Monotoniczność to za mało. u_n+1/u_n < 1 nie wystarcza Np. dla u_n=n/(n+1) mamy u_n+1/u_n < 1, ale u_n →1.

jc: Oj, to nakombinowane rozwiązanie, a uzasadnienie jest proste (podałem wyżej).

jc: Jeśli u_n →g, to u_n+1 →g. To ten sam ciąg tylko z pominiętym pierwszym wyrazem. Domyślam się, że autor chce powołać w ten sposób dojść do sprzeczności. Gdyby g>0, to g_n+1/g_n →1, a wiemy, że tak nie jest. Dowód nie podpowiada, jak szybko ciąg zmierza do 0, a zastosowaniach ma to często duże znaczenie (kiedyś poznasz kryterium zbieżności szeregów d'Alamberta).

Shizzer: Dziękuję Ci bardzo za pomoc jc. Jutro sobie przestudiuję Twój dowód, jak czegoś nie zrozumiem to będę pytał, bo ten dowód jest dla mnie dość trudny szczerze mówiąc