zadanie z logarytmów na poziomie rozszerzonym krzychu: Proszę o pomoc w rozwiązaniu zadania 174. b) log₂(3^x+1 + 1) > 1 + log₂(9^x − 2) wyznaczam dziedzinę: D: 3^x+1 + 1 > 0 ∧ 9^x − 2 > 0 ⇔ x ∊ R ∧ 9^x > 2 log₂(3^x+1 + 1) > 1 + log₂(9^x − 2) log₂(3^x+1 + 1) > log₂2 + log₂(9^x − 2) log₂(3^x+1 + 1) > log₂[2(9^x − 2)] 3^x+1 + 1 > 2*9^x − 4 niech 3^x = t, t>0 wtedy: 3t + 1 > 2t² − 4 2t² − 3t − 5 < 0 Δ = 49 √Δ = 7 t₁ = 5/2 t₂ = −1 ∧ t>0 ⇒ t₂ ∊ ∅ 3^x = 5/2 ⇒ log₃5/2 = x I teraz nie wiem za bardzo, co mam dalej zrobić. Wiem, że powinien wyjść przedział, jeden pierwiastek to log₃5/2, ale co z drugim? Podejrzewam, że popełniłem gdzieś błąd. Odpowiedź to x ∊ (log₂√2, log₃5/2)

Słoniątko: nie pisz t∊∅ kto was tak uczy? rozwiązuj nierówność do końca i przecinaj rozwiązanie z warunkiem t>0

a7: nie jestem pewna, ale w dziedzinie x∊(log₃√2,∞)

	5
a tam, gdzie masz podstawienie t x∊(−∞, log3 (		))
	2

	5
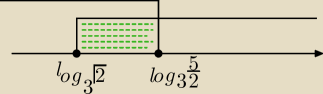
i w części wspólnej z dziedziną wychodzi x∊(log3√2,log3 (		))
	2

(?)

a7: tak wyszło mi dobrze https://www.wolframalpha.com/input/?i=+log2%283%5E%7Bx%2B1%7D+%2B+1%29+%3E+1+%2B+log2%289%5Ex+%E2%88%92+2%29

krzychu: Dziękuję bardzo a7! Bardzo było to pomocne, w porównaniu do użytkownika Słoniątko, który zamiast pomóc, zastanawia się kto uczy pisać t∊∅... Nie o tym było zadanie XD

6latek: I ma racje co do tego napewno uczyl Cie takiego zapisu nauczyciel? czy sam gdzies przeczytales w internetach? jesli nie jestes pewien jak uzywac taich zapisow to ich nie uzywaj jesli wyszlo t=−1 to nalezalo napisac (Nie nalezy do rozwiazan )

Damian#UDM: Czemu nie można tak zapisać? Dziedzina dla t to (0, ∞) t₂=−1 , czyli t₂ nie należy do dziedziny (0, ∞) równanie to jest sprzeczne, nie można tego zapisać w ten sposób? t₂ ∊ ∅ czemu?